插入、希尔、选择、堆排序
前言
代码位置
gitee
排序方法
常见排序算法
本篇介绍前四种,在之后博客中会讲到交换排序和归并排序以及计数排序

插入排序
直接插入排序
基本思想
直接插⼊排序是⼀种简单的插⼊排序法,其基本思想是:把待排序的记录按其关键码值的⼤⼩逐个插⼊到⼀个已经排好序的有序序列中,直到所有的记录插⼊完为⽌,得到⼀个新的有序序列。
- 实际我们玩扑克牌时就用到了这一思想

动图理解:
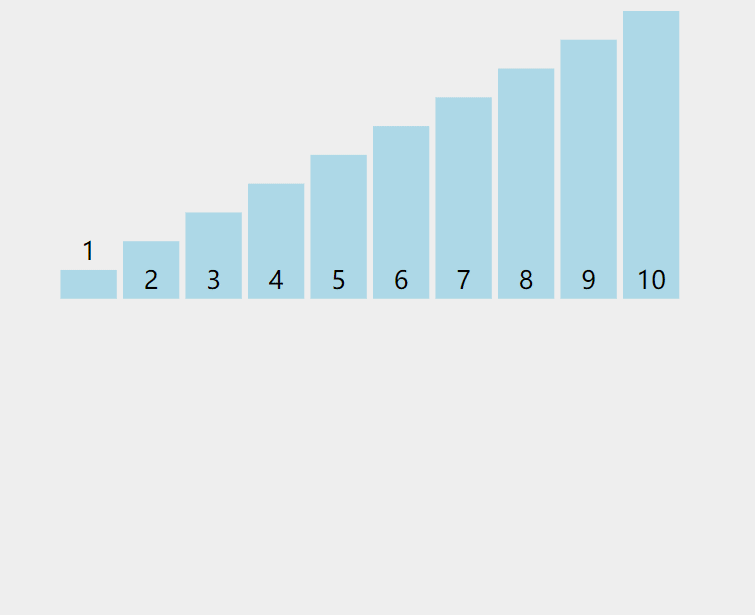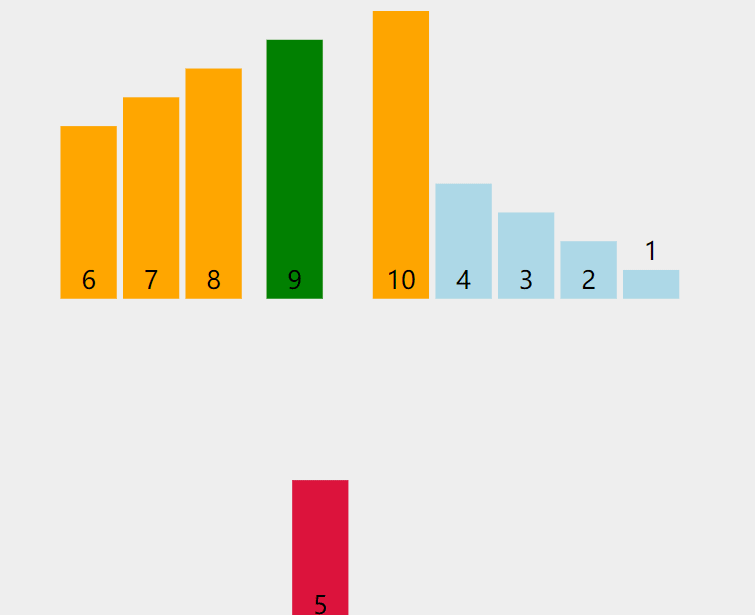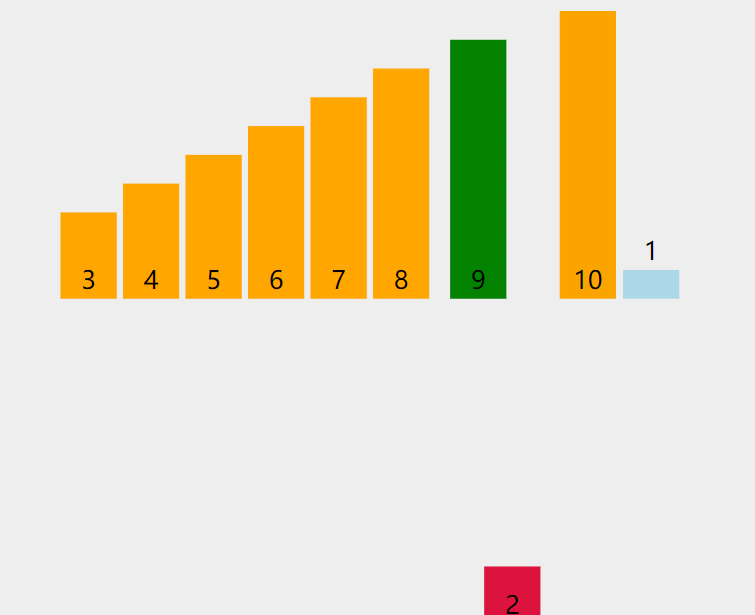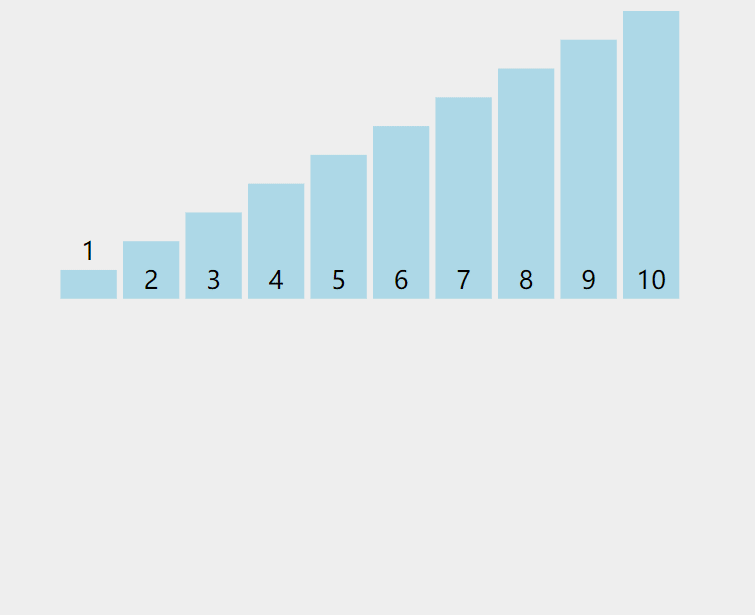
- 当插⼊第 i(i>=1) 个元素时,前⾯的 array[0],array[1],…,array[i-1] 已经排好序,此时⽤ array[i] 的排序码与 array[i-1],array[i-2],… 的排序码顺序进⾏⽐较,找到插⼊位置即将 array[i] 插⼊,原来位置上的元素顺序后移
- 以排序数组为例:
inta[]={ 5,3,9,6,2,4,7,1,8};
- 由以上分析可以定义两个参数
- end:指向有序序列的最后一个数据,显然:
- tmp:有序序列后的第一个待排序数据,显然
- 以一次循环为例:
- 将tmp与end位置数据进行比较,
- 若end处更大,需要将end位置数据移到end+1处,end–,继续让end-1处数据与tmp比较
- 否则直接跳出循环,此时end+1位置为空,需要放入tmp
- 最坏的情况:当end为0处数据移到end为1处,此时end变为-1,需要跳出循环,并将tmp放到0处
结合以上分析,很容易写出代码:
voidInsertSort(int*arr,intn){ for(inti =0;i <n -1;i++){ intend =i;inttmp =arr[end +1];while(end >=0){ if(arr[end]>tmp){ arr[end +1]=arr[end];end--;}else{ break;}}arr[end +1]=tmp;}}
时间复杂度分析:
空间复杂度:O(1)
希尔排序
在直接插入排序中我们发现,元素越无序,直接插入排序算法时间效率越低(因为比较次数越多)。特别是当数组为降序,我们要排升序,此时数组的相对无序程度达到了最大,时间复杂度也到了最大
所以我们有没有办法对这样一种情况进行优化呢?
答案就是希尔排序,它由D.L.Shell在1959年提出,也是第一批时间复杂度突破了O(n2)的算法之一(致敬🫡)
- 希尔排序是基于插入排序的以下两点性质而提出改进方法的:
插入排序在对几乎已经排好序的数据操作时,效率高,即可以达到线性排序的效率。
但插入排序一般来说是低效的,因为插入排序每次只能将数据移动一位。
基本思想:
希尔排序法⼜称缩⼩增量法。
希尔排序法的基本思想是:先选定⼀个整数(通常是gap=n/3+1),把 待排序⽂件所有记录分成各组,所有的距离相等的记录分在同⼀组内,并对每⼀组内的记录进⾏排序,然后gap=gap/3+1得到下⼀个整数,再将数组分成各组,进⾏插⼊排序,当gap=1时,就相当于直接插⼊排序。它是在直接插⼊排序算法的基础上进⾏改进⽽来的,综合来说它的效率是要⾼于直接插⼊排序算法的。
- 以排序数组为例:(这里我们取的gap=2演示一下)

- 既然是直接插入排序法的改进,二者在许多地方有相似之处:
- 一次预排序
- 从下标为0的元素开始,每隔gap-1个数据取数据分到一组,从取数据的方式我们可以得出以下结论:
- 总共有gap组(0-(gap-1)的元素为每一组的头元素)
- 每组有n/gap或n/gap+1个数据
- 每一次排序我们排的是end和end+gap(即tmp)处的元素,保证每次排序都是在同一组内排
- end初始为0可得tmp初始为gap,tmp末态为n-1可得end末态为n-1-gap
- 在一组内进行的是直接插入排序,只不过把距离从1换为gap,全部换一下就行了,思路是一样的
- 每次预排序结束后,让gap/3+1
- 加一保证最后一次排序gap为1,否则无法保证最后一次是直接插入排序
voidShellSort(int*arr,intn){ intgap =n;while(gap >1){ gap =gap /3+1;for(inti =0;i <n -gap;i++){ intend =i;inttmp =arr[end +gap];while(end >=0){ if(arr[end]>tmp){ arr[end +gap]=arr[end];end -=gap;}else{ break;}}arr[end +gap]=tmp;}}}
时间复杂度分析:
外层循环的时间复杂度可以直接给出为:O(log2n) 或者O(log3n) ,即O(logn)

假设⼀共有n个数据,合计gap组,则每组为n/gap(大致)个;在每组中,插⼊移动的次数最坏的情况下为 S=1 + 2 + 3 + ……+ (n/gap-1),⼀共是gap组,因此:
总计最坏情况下移动总数为:gap ∗ S
gap取值有(以除3为例):n/3 n/9 n/27 … 2 1
一一带入
- 当gap为n/3时,移动总数为: n
- 当gap为n/9时,移动总数为: 4n
- 最后⼀趟,数组已经已基本有序了,gap=1即直接插⼊排序,移动次数就是n
- 通过以上的分析,可以画出这样的曲线图:

因此,希尔排序在最初和最后的排序的次数都为n,即前⼀阶段排序次数是逐渐上升的状态,当到达某⼀顶点时,排序次数逐渐下降⾄n,⽽该顶点的计算暂时⽆法给出具体的计算过程
- 内外循环综合来看,外层循环总共log3n次,内层循环的每次排序次数暂时无法精确计算,所以其复杂度不好计算。
希尔排序时间复杂度不好计算,因为 gap 的取值很多,导致很难去计算,因此很多书中给出的希尔排序的时间复杂度都不固定。《数据结构(C语⾔版)》—严蔚敏书中给出的时间复杂度为:

选择排序
基本思想
每⼀次从待排序的数据元素中选出最⼩(或最⼤)的⼀个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。
直接选择排序
- 在元素集合 array[i]–array[n-1] 中选择关键码最⼤(⼩)的数据元素
- 若它不是这组元素中的最后⼀个(第⼀个)元素,则将它与这组元素中的最后⼀个(第⼀个)元素交换
- 在剩余的 array[i]–array[n-2](array[i+1]–array[n-1]) 集合中,重复上述步 骤,直到集合剩余1个元素
动图解释:
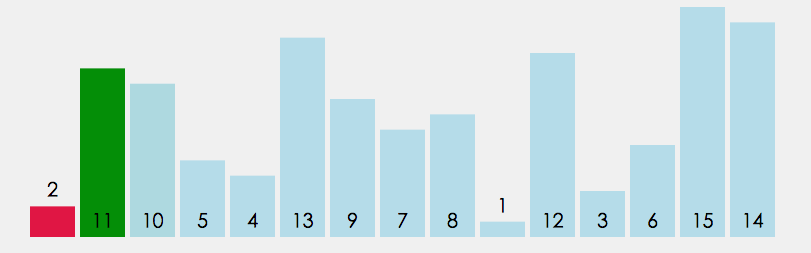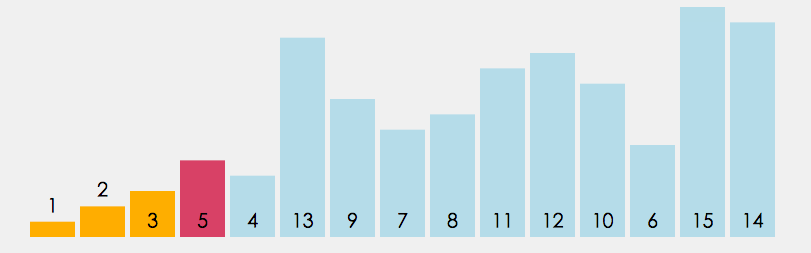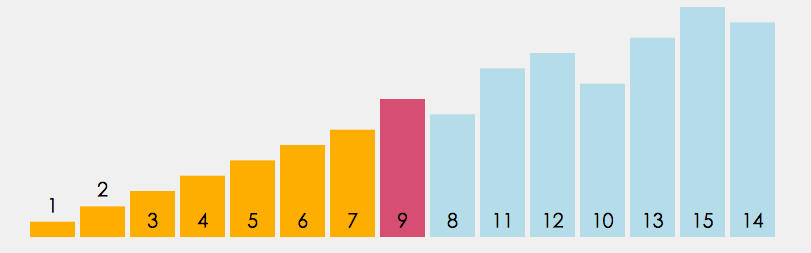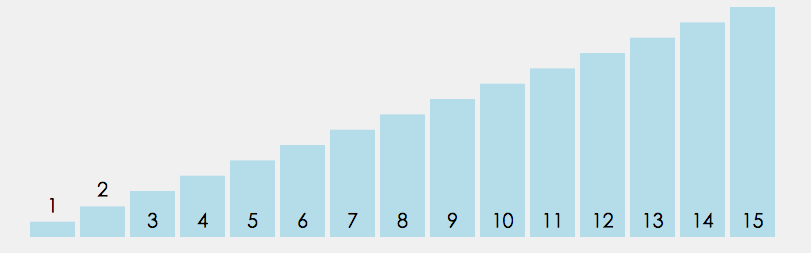
- 很容易写出如下代码:
- 排升序,每次在剩余序列中找最小的交换至前面
voidSelectSort1(int*arr,intn){ for(inti =0;i <n;i++){ intmini =i;for(size_tj =i+1;j <n;j++){ if(arr[j]<arr[mini])mini =j;}Swap(&arr[i],&arr[mini]);}}
- 进一步优化,每次在剩余序列中找最大的和最小的,最大的交换至后面,最小的交换至前面
voidSelectSort(int*arr,intn){ intbegin =0;intend =n -1;while(begin <end){ intmini =begin,maxi =begin;for(inti =begin+1;i <=end;i++){ if(arr[i]>arr[maxi]){ maxi =i;}if(arr[i]<arr[mini]){ mini =i;}}Swap(&arr[mini],&arr[begin]);Swap(&arr[maxi],&arr[end]);++begin;--end;}}
改进如下:
if(maxi ==begin){ maxi =mini;}
- 这样当我们将mini和begin交换完成后,maxi所指向的仍然是最大的数据,将其再与end交换
完整代码:
voidSwap(int*x,int*y){ inttmp =*x;*x =*y;*y =tmp;}voidSelectSort(int*arr,intn){ intbegin =0;intend =n -1;while(begin <end){ intmini =begin,maxi =begin;for(inti =begin +1;i <=end;i++){ if(arr[i]>arr[maxi]){ maxi =i;}if(arr[i]<arr[mini]){ mini =i;}}if(maxi ==begin){ maxi =mini;}Swap(&arr[mini],&arr[begin]);Swap(&arr[maxi],&arr[end]);++begin;--end;}}
直接选择排序的特性总结:
- 直接选择排序思考⾮常好理解,但是效率不是很好。实际中很少使用
- 时间复杂度:O(n2)
- 空间复杂度:O(1)
堆排序
基本思想
堆排序(Heapsort)是指利⽤堆积树(堆)这种数据结构所设计的⼀种排序算法,它是选择排序的⼀ 种。它是通过堆来进⾏选择数据。需要注意的是排升序要建⼤堆,排降序建⼩堆。
在堆的应用(堆排序与Top-K问题)已经讲过了此方法,这里就不赘述了。
以上就是插入、希尔、选择、堆排序的介绍啦,各位大佬有什么问题欢迎在评论区指正,您的支持是我创作的最大动力!❤️
