个人主页 ： 个人主页。
个人专栏 ： 数据结构 《C语言》《C++》《算法》。

文章目录。

• 前言。
• 一、题目分析。
• 二、解题思路。
• • 解题思路。
  • 状态表示。
  • 状态转移方程。
  • 初始化。
  • 填表顺序。
  • 返回值。
• 三、实现代码。
• 总结。

前言。

这篇文章只是我作为小白的一些理解，，如果有错误，，希望大佬们能指出。

918. 环形子数组的最大和。

一、题目分析。

连续子数组在求环型数组中最大和。

二、解题思路。

解题思路。

最大子数组和，有两种情况。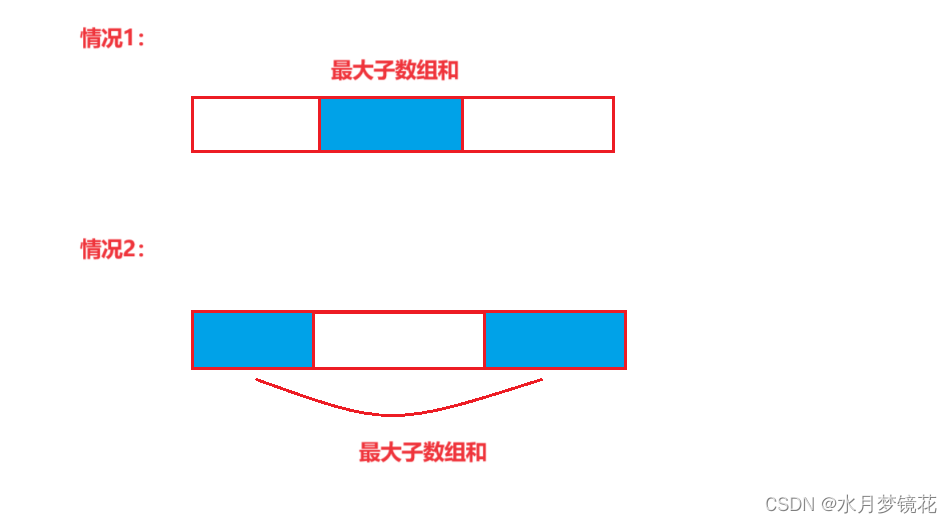

情况1，我们只需要正常使用dp来寻求最大子数组和。
对于情况2，假如我们用前缀和 与 后缀和 求和来求最大子数组和相对麻烦，但是如果我们要求最小子数组和#xff1f;

情况二：寻求最大子数组和，它可以转换为数组和(sum) - 最小子数组和。

状态表示。

问题的状态表示：经验(以这个位置为终点 / 以这个位置为起点) + 题目要求。

所以情况1记为。 f()。，f [ i ]表示以 i 子数组的最大和位于终点。
所以情况2记为。 g()。，g [ i ]表示以 i 子数组的最小和位置为终点。

状态转移方程。

情况1。
对于在数组 i 位置元素，我们可以把它分成两种状态。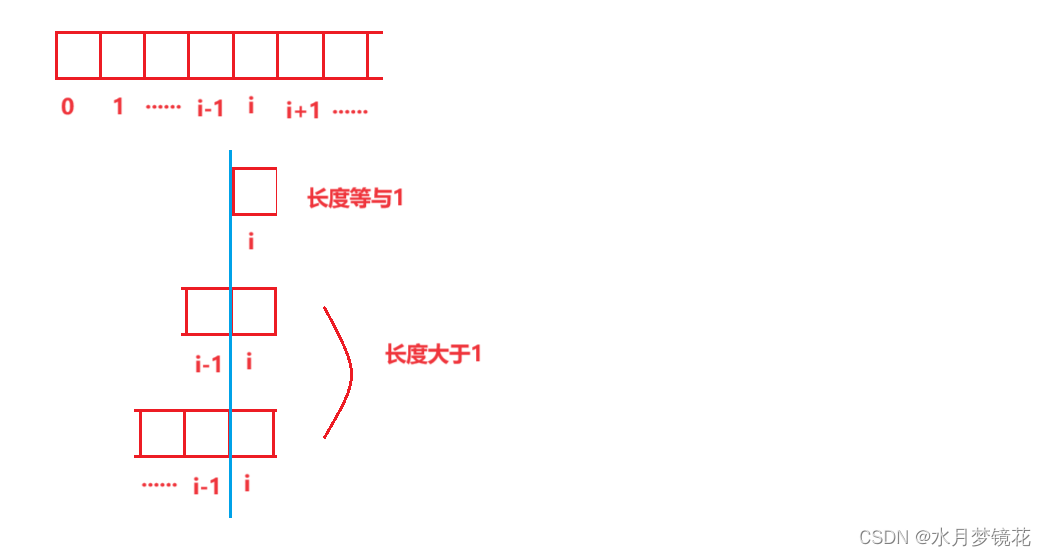

即 f [i]长度等于1，和 f [i]长度大于1。
当 f [i]长度等于1点，此时子数组最大的和不是该元素的大小，即f [i] = nums[i]。
当 f [i]长度大于1点，这个时候子数组最大的和不是吗？ 以前子数组最大和(f[i-1]) + 该元素的大小󿀌即f[i] = f[i-1] + nums[i]。
所以我们可以在这两种情况下获得最大值 f [ i ] 状态转移方程。

情况2。
和情况1类似󿀌情况2，我们也可以 位置，分为两种状态。

即 g [i]长度等于1，和 g [i]长度大于1。
当 g [i]长度等于1点，此时子数组的最小和不是该元素的大小，即g [i] = nums[i]。
当 g [i]长度大于1点，此时子数组最小，不是吗？ 以前子数组最小和(g[i-1]) + 该元素的大小󿀌即g[i] = g[i-1] + nums[i]。
然后我们将这两种状态的最小值󿀌既可以得到 g [i]状态转移方程。

初始化。

我们要求 f [i]就要先知道 f [i -1]，但如果当 i = 0点，f [i-1]会越界。然后我们虚拟一个空间�将整个 f[i] 向后移动一个位置。如下所示：

如果我们做这个操作，有两点需要注意。

• 如何填写 f[0]确保后续填表结果正确？
  只要f[0] = 0可以，毕竟f[1] = max(f[0], f[0]+nums此时f[0] == f[0] + nums[0]。
• 映射关系。
  因为整个f[i]后移一个，所以f[i] 对应元素 nums[i]相对向前移动，即f[i] 与 nums[i-1]元素对应。

填表顺序。

要求f[i]，首先要知道f[i-1]，然后，我们必须从前到后经历数组nums�来填表。

返回值。

我们只需要 返回情况1 与 情况2 最大值可以。
但对于{ -1, -2, -3, -就#xfff0而言c;情况2 值为：sum(-10) - gmin等于0࿰(-10)c;情况1 值为：fmax(-1)。那么返回值是0，结果错误。因此，首先要判断gminin == sum，如果相等�这意味着此时的数组都是负数，返回fmax即可。如果不相等󿀌返回情况1 与 情况2 最大值可以。

三、实现代码。

class。Solution。{ 。f。[。i。]。=max。(。f。[。i。-。1。]。+nums。[。i。-。1。]。,nums。[。i。-。1。]。)。;fmax。 =max。(。f。[。i。]。,fmax。)。;g。[。i。]。=min。(。g。[。i。-。1。]。+nums。[。i。-。1。]。,nums。[。i。-。1。]。)。;gmin。 =min。(。g。[。i。]。,gmin。)。;sum。 +=nums。[。i。-。1。]。;}。return。sum。 ==gmin。?。fmax。:。max。(。fmax。,sum。 -。gmin。)。;}。}。;

总结。

以上是我对环形子数组最大的理解。感谢您的支持󿀑！！