如果你喜欢这篇文章
发布时间:2025-06-24 20:45:54 作者:北方职教升学中心 阅读量:255
他们已经是两个有序的数组,
最后一步是两个数组每个元素的比例大小,然后将尾部插入临时数组,最后复制回来
要点:
第一个数比大小 2 > 0 所以尾插 0 让第二个数组下标begin2++,
因为这两个是升序数组,2 > 0,也表明 2 之后的一切都大于 0 ,
所以这里有 4 ( mid + 1,也就是第一个数组的长度) 逆序数对,
所以,当 2 和 4 比较,2 < 4 ,就尾插 2 临时数组,让第一组下标begin1++,
此时�继续比较5 > 4, 尾插 4 让第二个数组下标begin2++,
因为这两个是升序数组,5 > 4,也表明 5 之后的一切都大于 4,
但是因为第一个数组已经是第二个数了,因此:
这里就有 3 ( mid + 1 - begin1 (也就是说,减去第一个数组的下标))逆序数对。
之后我会输出更多高质量的内容欢迎收看。目录。,欢迎点赞和评论写下你的意见。如果你喜欢这篇文章,
我们以这个数组合并到最后一步为例:
[ 2, 5, 6, 7 ] 和 [ 0, 1, 4, 5 ]。
综上所述,
最后:
以上是本文的内容,感谢您的阅读。
最后:
以上是本文的内容,谢谢你的阅读。
如果你想和我一起学习编程点击关注,让我们一起学习#xff00c;一同成长。不明白为什么,
实际上,这个想法是利用合并排序的特点,具体思路如下:
例子: 数组 [ 7, 5, 2, 6, 0, 1, 5, 4 ]。
题目:剑指 Offer 51. 数组中的逆序对 - 扣除(Leetcode)
主题界面:
解题思路:
代码:
过了!!!
最后:
题目:剑指 Offer 51. 数组中的逆序对 - 扣除(Leetcode)
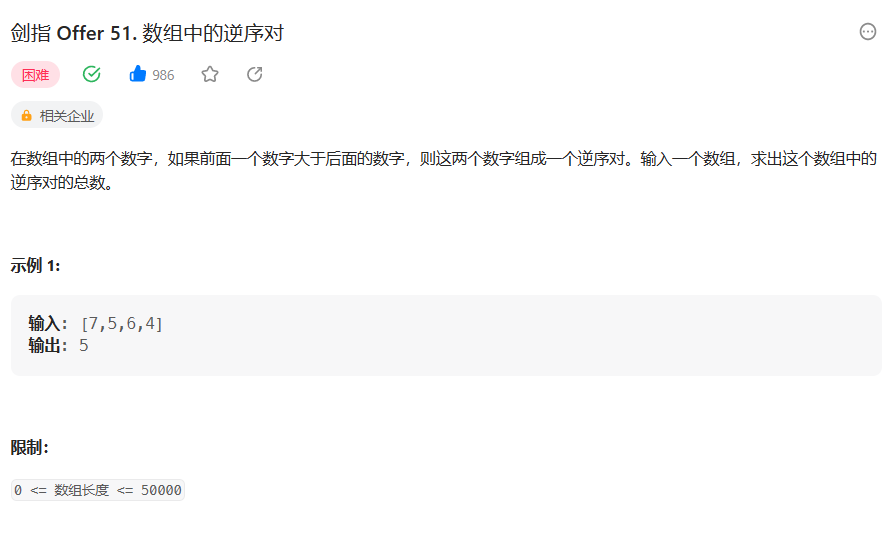
主题界面:
class Solution {public: int reversePairs(vector<int>& nums) { }};解题思路:
这个问题我的想法是用双指针暴力求解,
但是这个数组的长度O(N^2)时间复杂性绝对不可能完成所有样本,
看了大佬的想法,合并排序,(如果不合并排序最好先学习)
刚开始看了很久,
以下是代码:
代码:
class Solution {public: //计数 int res = 0; int reversePairs(vector<int>& nums) { //创建临时数组 vector<int> tmp(nums.size()); //分并排序,我用的是我学的并购排序模板 merge_sort(nums, tmp, 0, nums.size() - 1); return res; }private: void merge_sort(vector<int>& nums, vector<int>& tmp, int begin, int end) { if(begin >= end) return; //返回 //分治 int mid = (begin + end) >> 1; merge_sort(nums, tmp, begin, mid); merge_sort(nums, tmp, mid + 1, end); //[begin][mid], [mid + 1][end] //两个数组的下标 int begin1 = begin, end1 = mid; int begin2 = mid + 1, end2 = end; ///临时数组下标 int i = begin; //比较大小后,通过之前的合并,尾部插入临时数组 while(begin1 <= end1 && begin2 <= end2) { if(nums[begin1] <= nums[begin2] { tmp[i++] = nums[begin1Ʊ+]; } else { tmp[i++] = nums[begin2++]; //计算本段逆序数对数//具体推导阅读文章的文本 res += mid + 1 - begin1; ///整个思路的核心 } } ///将未插入值的所有尾部插入临时数组 while(begin1 <= end1) tmp[i++] = nums[begin1Ʊ+]; while(begin2 <= end2) tmp[i++] = nums[begin2++]; ///将临时数组复制回原数组 for(int i = begin; i <= end; i++) { nums[i] = tmp[i]; } }};
过了!!!
 。
。
我们只需要第一个数组的值 > 第二个数组的值,记录逆序数对 (mid + 1 - begin1) 即可。
