发布时间:2025-06-24 17:16:42 作者:北方职教升学中心 阅读量:151
- 对于节点 0 ,我们不需要任何时间,因为它就是我们的起点。
提示:
1 <= n <= 5 * 1040 <= edges.length <= 105edges[i] == [ui, vi, lengthi]0 <= ui, vi<= n - 11 <= lengthi<= 105disappear.length == n1 <= disappear[i] <= 105
解题方法:单源最短路的Dijkstra算法
关于
单源最短路的Dijkstra算法的视频讲解,可以查看这个视频。同时给你一个数组
disappear,其中disappear[i]表示节点i从图中消失的时间点,在那一刻及以后,你无法再访问这个节点。- 时间复杂度O ( n + m log m ) O(n+m\log m) O(n+mlogm),其中n n n是节点数量,m m m是边的数量。
每次从优先队列中取出一个元素,这样就得到了这个元素的最快到达时间。以此节点开始将所有相邻的没有确定过最短时间的节点入队。很简单,在每次遍历当前节点的相邻节点时,若无法在某相邻节点消失之前到达,则不将其入队。
请你返回数组
answer,answer[i]表示从节点0到节点i需要的 最少 单位时间。- 对于节点 0 ,我们不需要任何时间,因为它就是我们的起点。
大致思路是:从起点开始,每次将所有的能一部到达的节点放入优先队列中。
关于本题,有个额外条件就是节点消失时间。
- 对于节点 1 ,我们需要至少 2 单位时间,通过
edges[0]到达。但当我们到达的时候,它已经消失了,所以我们无法到达它。优先队列中存放的是每个节点的首次能到达的时间以及节点编号,能最先到达的最先出队。示例 1:
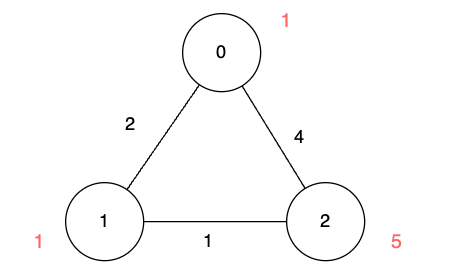
输入:n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,1,5]
输出:[0,-1,4]
解释:
我们从节点 0 出发,目的是用最少的时间在其他节点消失之前到达它们。直到队列为空为止,就得到了从起点到其他任意一点的最短耗时。
【LetMeFly】3112.访问消失节点的最少时间:单源最短路的Dijkstra算法
力扣题目链接:https://leetcode.cn/problems/minimum-time-to-visit-disappearing-nodes/
给你一个二维数组
edges表示一个n个点的无向图,其中edges[i] = [ui, vi, lengthi]表示节点ui和节点vi之间有一条需要lengthi单位时间通过的无向边。示例 3:
输入:n = 2, edges = [[0,1,1]], disappear = [1,1]
输出:[0,-1]
解释:
当我们到达节点 1 的时候,它恰好消失,所以我们无法到达节点 1 。
- 空间复杂度O ( n + m ) O(n+m) O(n+m)
AC代码
C++
classSolution{public:vector<int>minimumTime(intn,vector<vector<int>>&edges,vector<int>&disappear){vector<vector<pair<int,int>>>graph(n);for(vector<int>&edge :edges){graph[edge[0]].push_back({edge[1],edge[2]});graph[edge[1]].push_back({edge[0],edge[2]});}vector<int>ans(n,-1);priority_queue<pair<int,int>,vector<pair<int,int>>,greater<>>pq;// [<time, toNode>, ...pq.push({0,0});while(pq.size()){auto[thisTime,thisNode]=pq.top();pq.pop();if(ans[thisNode]!=-1){continue;}ans[thisNode]=thisTime;for(auto[nextNode,length]:graph[thisNode]){if(ans[nextNode]!=-1||thisTime +length >=disappear[nextNode]){continue;}pq.push({thisTime +length,nextNode});}}returnans;}};Java
importjava.util.ArrayList;importjava.util.Arrays;importjava.util.List;importjava.util.PriorityQueue;importjava.util.Queue;classSolution{publicint[]minimumTime(intn,int[][]edges,int[]disappear){List<int[]>[]graph =newArrayList[n];Arrays.setAll(graph,i ->newArrayList<>());for(int[]edge :edges){graph[edge[0]].add(newint[]{edge[1],edge[2]});graph[edge[1]].add(newint[]{edge[0],edge[2]});}int[]ans =newint[n];Arrays.fill(ans,-1);Queue<int[]>pq =newPriorityQueue<>((a,b)->(a[0]-b[0]));pq.add(newint[]{0,0});while(!pq.isEmpty()){int[]temp =pq.poll();intthisTime =temp[0];intthisNode =temp[1];if(ans[thisNode]!=-1){continue;}ans[thisNode]=thisTime;for(int[]temp2 :graph[thisNode]){intnextNode =temp2[0];intlength =temp2[1];if(ans[nextNode]==-1&&thisTime +length <disappear[nextNode]){pq.add(newint[]{thisTime +length,nextNode});}}}returnans;}}Python
fromtyping importListimportheapqclassSolution:defminimumTime(self,n:int,edges:List[List[int]],disappear:List[int])->List[int]:graph =[[]for_ inrange(n)]forx,y,d inedges:graph[x].append((y,d))graph[y].append((x,d))ans =[-1]*n pq =[(0,0)]whilepq:thisTime,thisNode =heapq.heappop(pq)ifans[thisNode]!=-1:continueans[thisNode]=thisTime fornextNode,length ingraph[thisNode]:# print(nextNode, length, ans[nextNode], thisTime + length, disappear[nextNode]) #------------------# print(ans[nextNode] != -1)# print(thisTime + length < disappear[nextNode])ifans[nextNode]==-1andthisTime +length <disappear[nextNode]:heapq.heappush(pq,(thisTime +length,nextNode))returnansif__name__ =='__main__':sol =Solution()print(sol.minimumTime(3,[[0,1,2],[1,2,1],[0,2,4]],[1,1,5]))同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/140530368
- 对于节点 2 ,我们需要至少 3 单位时间,通过
edges[0]和edges[1]到达。 - 对于节点 2 ,我们需要至少 4 单位时间,通过
edges[2]到达。如果从节点0出发 无法到达节点i,那么answer[i]为-1。注意,图有可能一开始是不连通的,两个节点之间也可能有多条边。
示例 2:
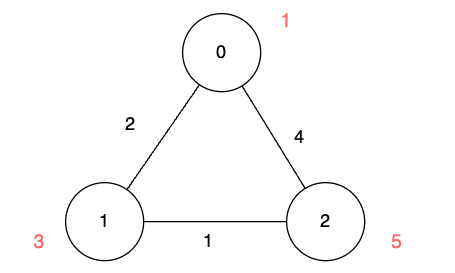
输入:n = 3, edges = [[0,1,2],[1,2,1],[0,2,4]], disappear = [1,3,5]
输出:[0,2,3]
解释:
我们从节点 0 出发,目的是用最少的时间在其他节点消失之前到达它们。
- 对于节点 0 ,我们不需要任何时间,因为它就是我们的起点。
- 对于节点 1 ,我们需要至少 2 单位时间,通过
edges[0]到达。
