发布时间:2025-06-24 18:59:28 作者:北方职教升学中心 阅读量:336
解法:
我们通过阅读题目可以发现要使整个链表两两交换 ,可以将大问题分为把1和2后面的节点两两交换,把一二交换即可,同理3和4也是同样的处理思路。
本例题代码实现如下:
class Solution { public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) { dfs(A,B,C,A.size()); } public void dfs(List<Integer> A, List<Integer> B, List<Integer> C,int n ){ if(n == 1){ C.add(A.remove(A.size() - 1)); return; } dfs(A,C,B,n - 1); C.add(A.remove(A.size() - 1)); dfs(B,A,C,n - 1); }}关于本例题要注意的点:c.add(a.remove(a.size() - 1));可能有的友友会纠结为什么不是remove(0)呢,其实自己模拟一下即可,我们移走盘子是从最上面那个盘子开始移动的。
2.相同子问题(函数头)
我们要设计一个函数头来完成汉诺塔的递归过程,我们可以看到我们需要三根柱子和要记录下来还剩下几个盘子。
代码如下:
class Solution { public ListNode mergeTwoLists(ListNode list1, ListNode list2) { if(list1 == null){ return list2; } if(list2 == null){ return list1; } if(list1.val <= list2.val){ list1.next = mergeTwoLists(list1.next,list2); return list1; }else{ list2.next = mergeTwoLists(list1,list2.next); return list2; } }}例题3:反转链表
链接:反转链表
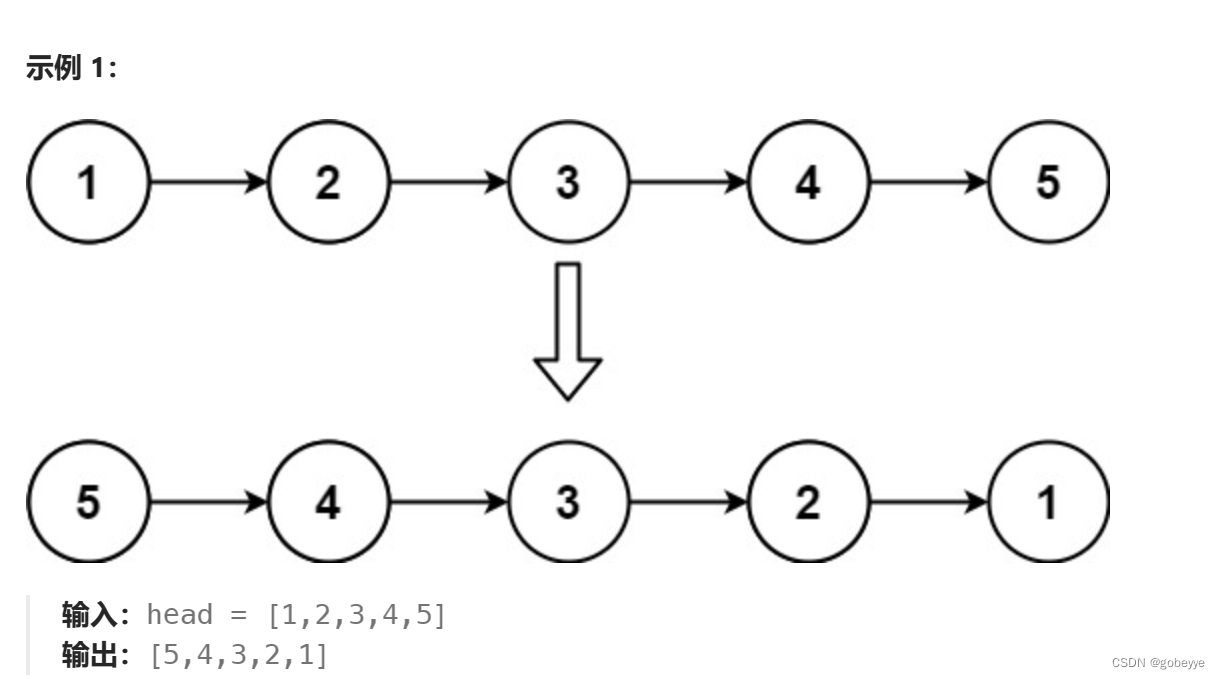
题目简介:
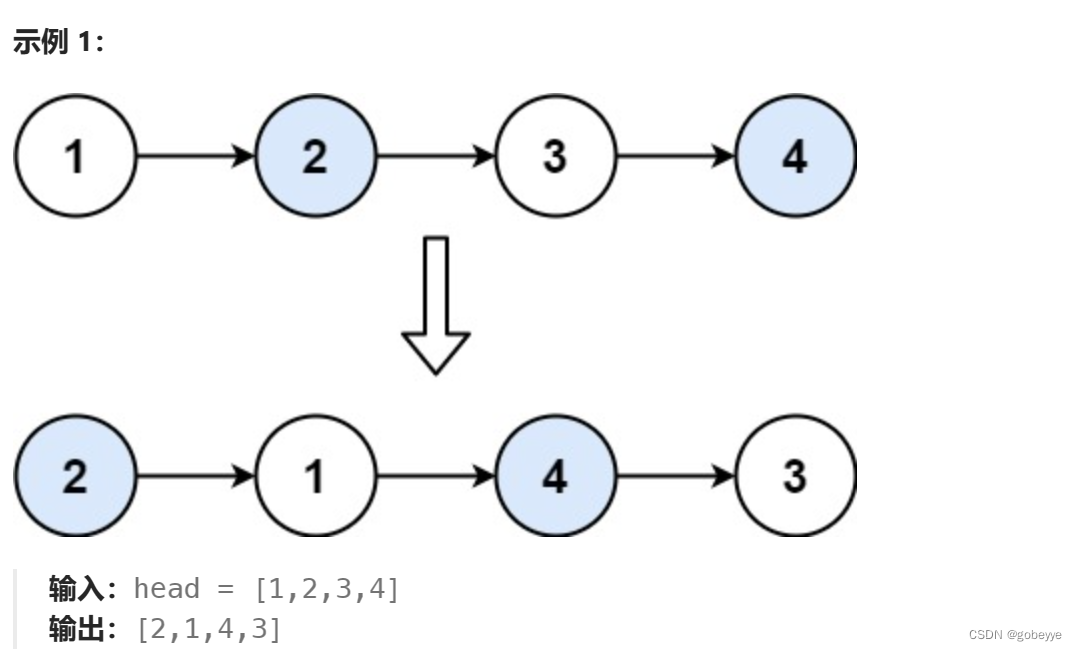
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
为什么会用到递归?
大问题可以拆解成相同的子问题,且子问题的解法和大问题的一模一样,这是就可以用到递归。
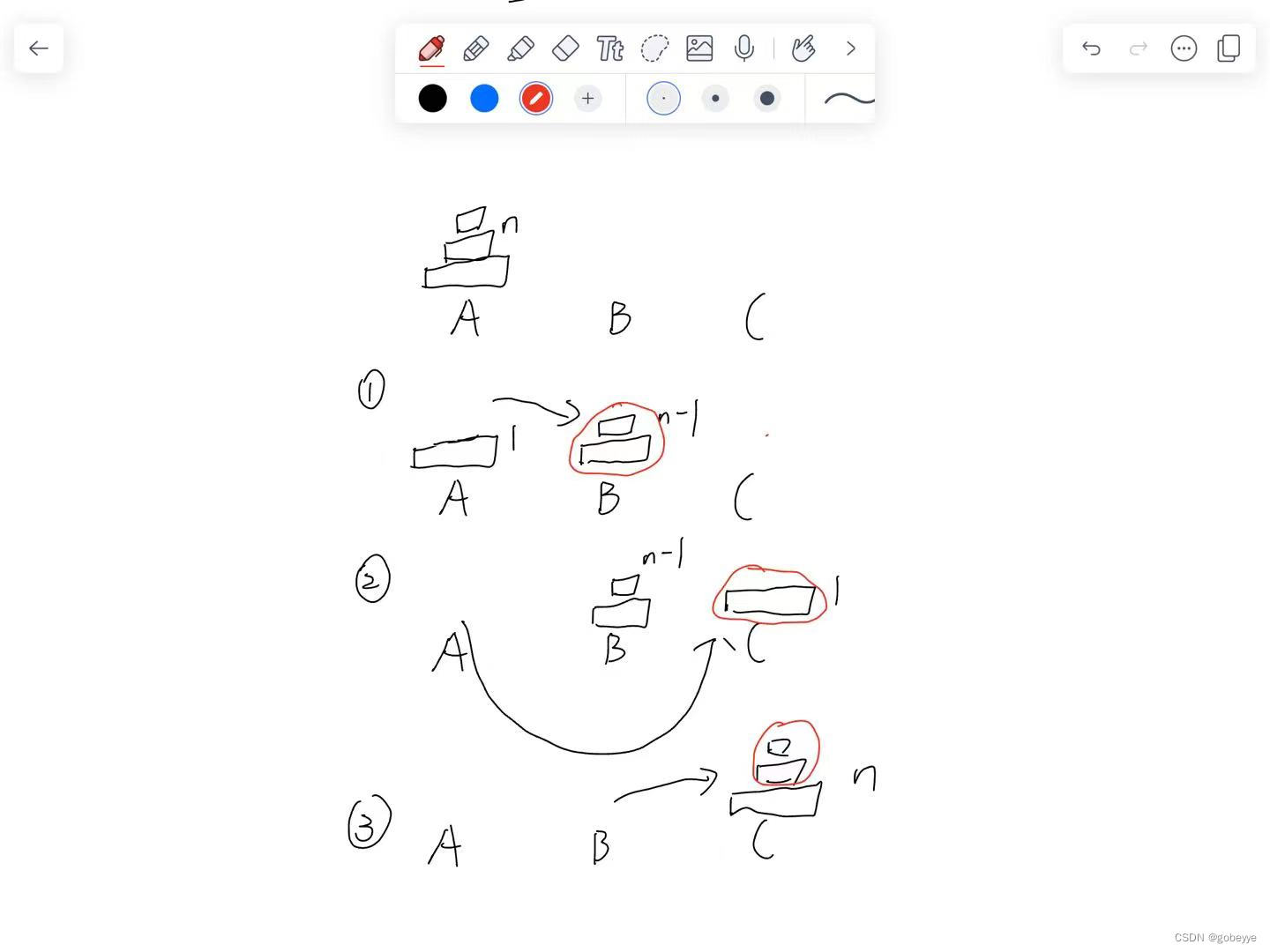
例题1:汉诺塔
链接:汉诺塔
题目简介:
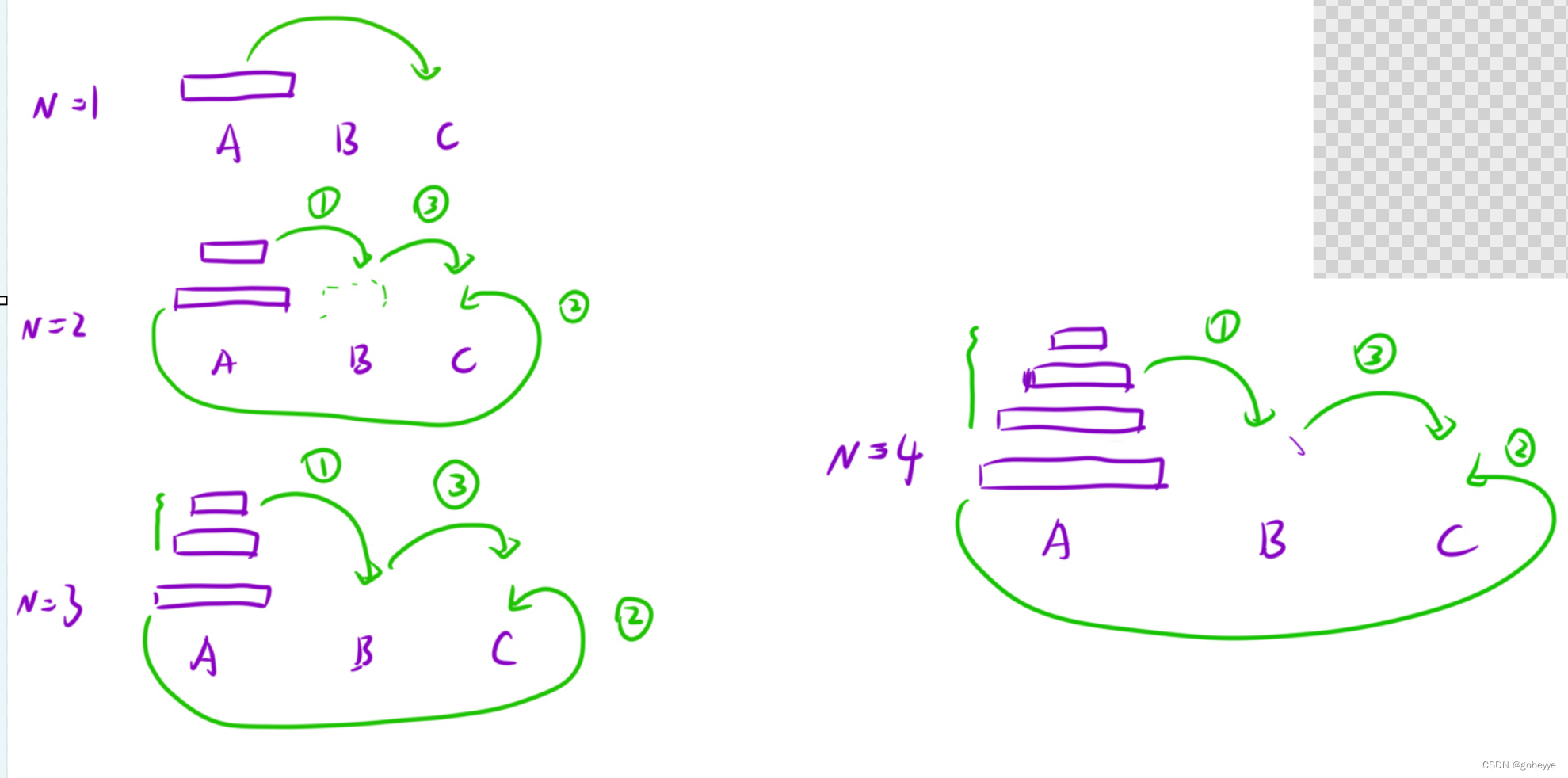
递归问题非常经典的一道题目,在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。
上述步骤可以通过数学归纳法来证明。
例题2:合并两个有序链表
链接:合并两个有序链表
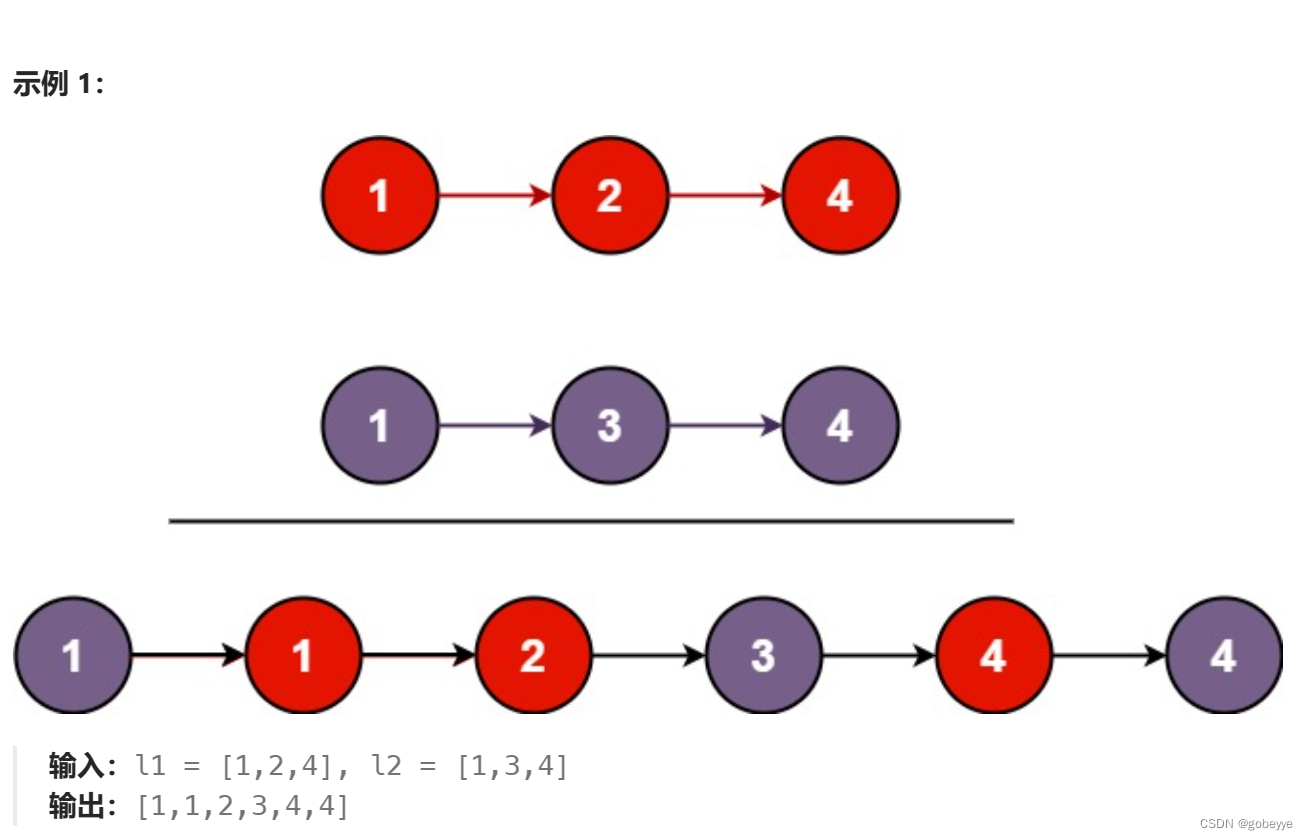
题目简介:
将两个升序链表合并为一个新的 升序 链表并返回。

解法:
这题不能使用1个1个数的分离递归(会超时),我们这里要采用二分的思路,具体实现如下:
1.递归函数的作用
求出x 的n 次⽅是多少,然后返回;
2.相同子问题(函数头)
需要传入需要n次方的x和n还要将其返回public double pow(double x, int n)
3.只关心某一个子问题是如何解决的(函数体)
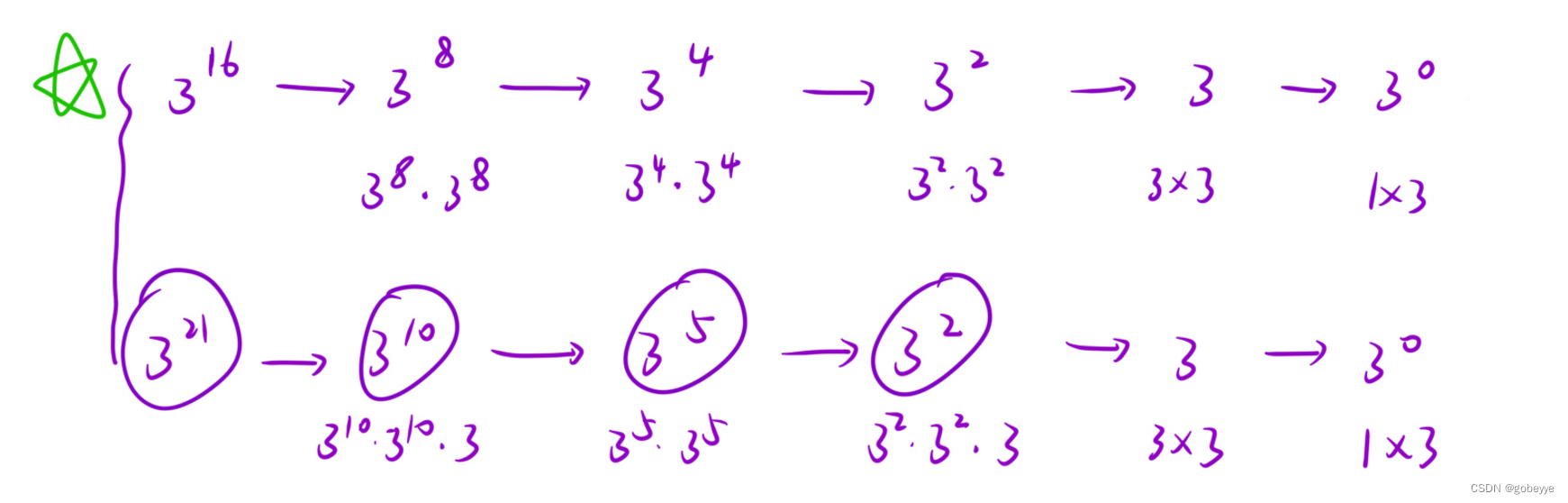
先求出x 的n / 2 次⽅是多少,然后根据n 的奇偶,得出x 的n 次⽅是多少;
4.递归出口
当n 为0 的时候,返回1 即可。
c. 存在⼀种简单情况,或者说当问题的规模⾜够⼩时,我们可以直接求解问题。
不用太深究函数的细节(陷入将无法自拔),如果是第一次的话可以去b站上看看递归的全过程细节(这里的不用深究是建立在已经对它的展开有一定理解了,第一次学汉诺塔的话我还是建议大家可以看看别人推的整个过程,理解更加深刻)。