——将待排序列调整成 

发布时间：2025-06-24 19:17:09  作者：北方职教升学中心  阅读量：170

——将待排序列调整成 。，或者随机确定；

/** * 归并排序 * * @param array * @return */public static int[] MergeSort(int[] array) {	if (array.length < 2) return array;	int mid = array.length / 2;	int[] left = Arrays.copyOfRange(array, 0, mid);	int[] right = Arrays.copyOfRange(array, mid, array.length);	return merge(MergeSort(left), MergeSort(right));}/** * 归并排序-将两个排序好的数组结合成一个排序数组 * * @param left * @param right * @return */public static int[] merge(int[] left, int[] right) {	int[] result = new int[left.length + right.length];	for (int index = 0, i = 0, j = 0; index < result.length; index++) {		if (i >= left.length)			result[index] = right[j++];		else if (j >= right.length)			result[index] = left[i++];		else if (left[i] > right[j])			result[index] = right[j++];		else			result[index] = left[i++];	}	return result;}。

def merge_sort(array):    if len(array) < 2:        return array    mid = len(array) // 2    left = array[:mid]    right = array[mid:]        return merge(merge_sort(left), merge_sort(right))def merge(left, right):    result = [0] * (len(left) + len(right))    i = j = index = 0    while index < len(result):        if i >= len(left):            result[index] = right[j]            j += 1        elif j >= len(right):            result[index] = left[i]            i += 1        elif left[i] > right[j]:            result[index] = right[j]            j += 1        else:            result[index] = left[i]            i += 1        index += 1    return result。——确定分界点。、以下是󿀌易于理解󿄚
代码实现。

void merge_sort(int q[], int l, int r){	// 1.判边界    if (l >= r) return;		// 2.定分界点    int mid = l + r + 1 >> 1;	// 递归排序子序列    merge_sort(q, l, mid - 1), merge_sort(q, mid, r);	// 3.合并排序（双指针法）    int k = 0, i = l, j = mid;    while (i <= mid - 1 && j <= r)        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];        else tmp[k ++ ] = q[j ++ ];    // 一个子序列走到了最后，添加另一个序列的剩余部分 tmp 中    while (i <= mid - 1) tmp[k ++ ] = q[i ++ ];    while (j <= r) tmp[k ++ ] = q[j ++ ];		// 将排序结果 tmp 重新覆盖掉 q    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];}。
原文链接：https://blog.csdn.net/qq_40430360/article/details/125420190。q[r]。

例如，

归并排序模板（背诵）

模板1：

void merge_sort(int q[], int l, int r){	// 1.判边界    if (l >= r) return;		// 2.定分界点    int mid = l + r >> 1;	// 递归排序子序列    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);	// 3.合并排序（双指针法）    int k = 0, i = l, j = mid + 1;    while (i <= mid && j <= r)        if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];        else tmp[k ++ ] = q[j ++ ];    // 一个子序列走到了最后，添加另一个序列的剩余部分 tmp 中    while (i <= mid) tmp[k ++ ] = q[i ++ ];    while (j <= r) tmp[k ++ ] = q[j ++ ];		// 将排序结果 tmp 重新覆盖掉 q    for (i = l, j = 0; i <= r; i ++, j ++ ) q[i] = tmp[j];}。
归并排序算法（Merge Sort）简介。
快速排序（Quick Sort）与࿰相比c;快速排序将序列分为两个子序列，再递归使子序列有序；归并排序首先使子序列有序，再合并。（三种常用方法）：q[l]。。。

[分析避免边界问题]。

算法的基本思想和过程（时间复杂度O(nlogn) ）

• Step1。q[(l+r)/2]。 两个子序列，递归排序 。right。 和 。

当递归取的 merge_sort(q, l, mid - 1), merge_sort(q, mid, r);，为了避免陷入死循环，取中间值需要上取整 x = q[l + r + 1 >> 1]。mid。right。

合并排序（#xff08;Merge Sort）它是一种基于合并操作的有效，稳定的排序算法，采用该算法 分治法（Divide and Conquer） 一个非常典型的应用。、将得到两个排序的子序列 list1 和 list2 ，采用 双指针算法 将其合二为一：

• 定义两个指针：i 和 j，分别指向两个子序列的起始元素，定义一个新的序列 temp 用于存储合并结果；
• 比较两个指针指向的元素：
•                 若 *i <= *j ，放入这个元素 temp 中，并且 i++ ；
•                 若 *i > *j ，放入这个元素 temp 中，并且 j++ ；
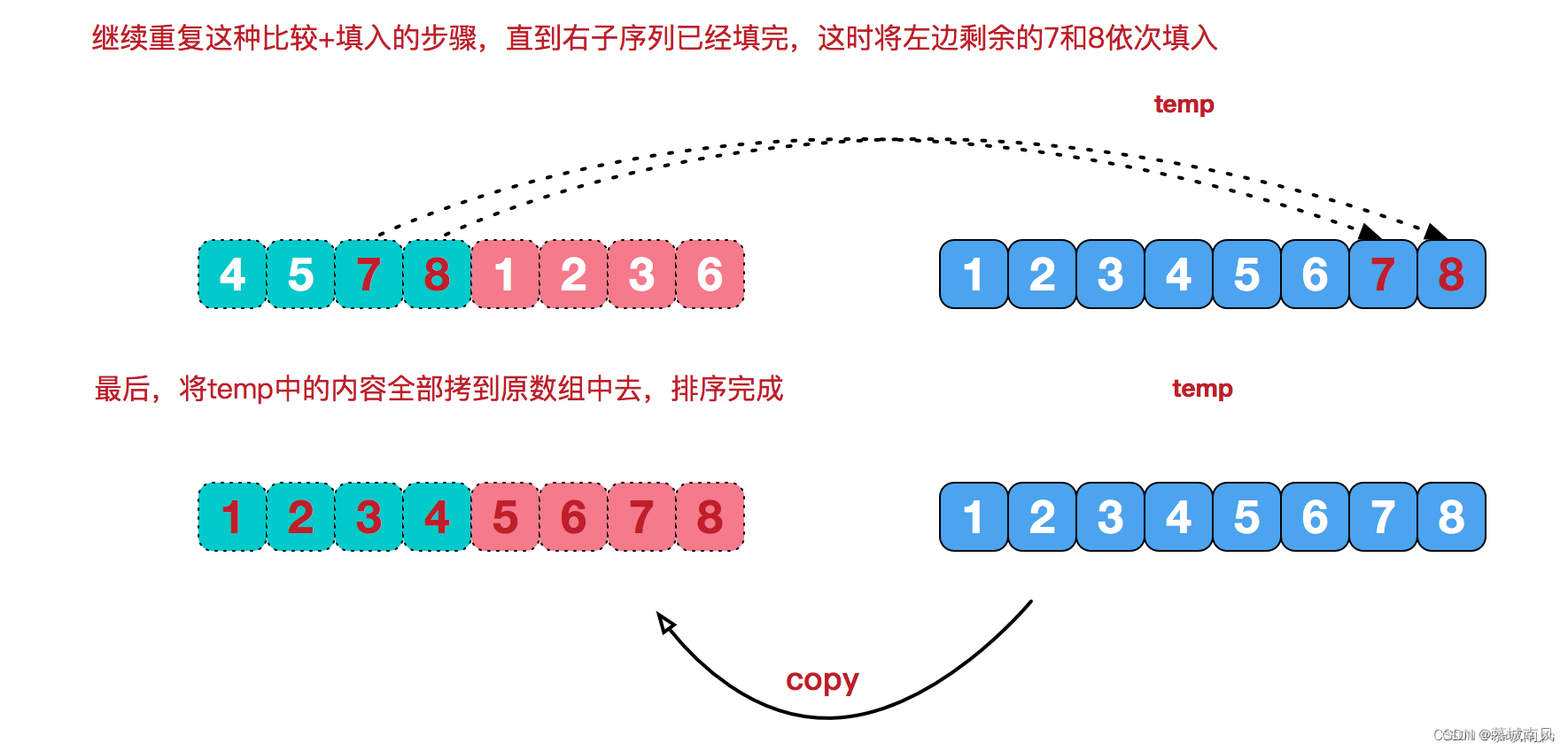
• 上述比较操作不断循环，直到某个指针指向子序列的末尾，将另一个序列的剩余部分按顺序放入 temp 中间可以，所得的 temp 这个序列是合并排序的结果。left。

  目录。 和 。