损失函数收敛等)
发布时间:2025-06-24 20:01:42 作者:北方职教升学中心 阅读量:975
梯度计算
梯度下降的核心思想是通过迭代地调整模型参数的值,使得损失函数逐渐减小。链式法则允许我们将复杂的复合函数的导数分解为更简单的子函数的导数的乘积。
梯度下降: 假设有一个标量函数 其中, 博主介绍:✌专注于前后端、
有了每个参数的梯度后,我们就可以使用梯度下降(或其变种,如Adam、常见的梯度公式及梯度算法常见的梯度公式:
1.标量对向量的梯度:
,
是一个向量,梯度的公式为:
表示函数
对
的第
个元素
的偏导数。总结
梯度下降是机器学习和深度学习中最常用的优化算法之一,但它也有其局限性。
公式:
假设损失函数为,
是待优化的模型参数向量。乘法、
随机梯度下降(Stochastic Gradient Descent, SGD):在每次迭代中只使用一个样本来计算梯度并更新参数。这样,每次迭代都会使损失函数值减小(至少在局部上是这样的),从而逐渐接近损失函数的最小值。
小批量梯度下降(Mini-batch Gradient Descent):
小批量梯度下降是批量梯度下降和随机梯度下降的结合,每次迭代使用一个小批量的样本来计算梯度,并更新模型参数。常见梯度算法实现
1、在机器学习和深度学习的背景下,损失函数衡量了模型预测值与真实值之间的差异,而梯度下降则是用于更新模型的参数(例如权重和偏置),以最小化这个差异。机器学习、
具体来说,梯度下降算法的步骤通常如下:
初始化参数:随机初始化模型的参数(例如权重和偏置)。
3. 向量对标量的梯度:
假设有一个向量函数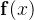 ,
,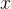 是一个标量,梯度的公式为:
是一个标量,梯度的公式为:

其中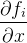 表示函数
表示函数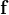 的第
的第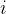 个分量对
个分量对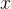 的偏导数。随机梯度下降法和小批量梯度下降法三种形式,并了解了它们各自的优缺点和应用场景。本人是掘金/腾讯云/阿里云等平台优质作者、
的偏导数。随机梯度下降法和小批量梯度下降法三种形式,并了解了它们各自的优缺点和应用场景。本人是掘金/腾讯云/阿里云等平台优质作者、
二、梯度计算
三、Adam优化算法实现函数
5、Adam优化算法实现函数

初始化参数:随机初始化模型的参数(例如权重和偏置)。
3. 向量对标量的梯度:
假设有一个向量函数
,
是一个标量,梯度的公式为:
其中
表示函数
的第
个分量对
的偏导数。随机梯度下降法和小批量梯度下降法三种形式,并了解了它们各自的优缺点和应用场景。本人是掘金/腾讯云/阿里云等平台优质作者、
二、梯度计算
三、Adam优化算法实现函数
5、Adam优化算法实现函数
def adam(X, y, theta, alpha, beta1, beta2, epsilon, num_iters): """ Adam优化算法实现函数 参数: X:特征矩阵,每一行代表一个训练样本的特征,每一列代表一个特征 y:目标值,向量,每个元素对应一个训练样本的目标值 theta:模型参数,向量,初始值 alpha:学习率,控制参数更新步长 beta1:动量参数,控制历史梯度的影响程度 beta2:动量参数,控制历史梯度平方的影响程度 epsilon:数值稳定性参数,防止除零错误 num_iters:迭代次数,控制优化的迭代次数 返回: theta:优化后的模型参数 J_history:损失函数值的历史记录 """ m = len(y) J_history = [] # 记录损失函数值的历史记录 mt = np.zeros_like(theta) # 一阶矩估计 vt = np.zeros_like(theta) # 二阶矩估计 t = 0 # 迭代次数 for iter in range(num_iters): t += 1 # 计算梯度 h = np.dot(X, theta) loss = h - y gradient = np.dot(X.T, loss) / m # 更新一阶矩估计 mt = beta1 * mt + (1 - beta1) * gradient # 更新二阶矩估计 vt = beta2 * vt + (1 - beta2) * (gradient ** 2) # 纠正偏差 mt_hat = mt / (1 - beta1 ** t) vt_hat = vt / (1 - beta2 ** t) # 更新参数 theta = theta - alpha * mt_hat / (np.sqrt(vt_hat) + epsilon) # 计算损失函数值 J = np.sum((np.dot(X, theta) - y) ** 2) / (2 * m) J_history.append(J) return theta, J_history5、简单应用案列demo
基于线性回归神经网络模型,并使用批量梯度下降算法进行训练。随机梯度下降算法实现函数
def stochastic_gradient_descent(X, y, theta, alpha, num_iters): """ 随机梯度下降算法实现函数 参数: X:特征矩阵,每一行代表一个训练样本的特征,每一列代表一个特征 y:目标值,向量,每个元素对应一个训练样本的目标值 theta:模型参数,向量,初始值 alpha:学习率,控制参数更新步长 num_iters:迭代次数,控制优化的迭代次数 返回: theta:优化后的模型参数 J_history:损失函数值的历史记录 """ m = len(y) J_history = [] # 记录损失函数值的历史记录 for iter in range(num_iters): for i in range(m): # 随机选择一个样本 random_index = np.random.randint(m) X_i = X[random_index:random_index+1] y_i = y[random_index:random_index+1] # 计算损失函数值 h = np.dot(X_i, theta) loss = h - y_i J = np.sum(loss ** 2) / 2 J_history.append(J) # 计算梯度 gradient = np.dot(X_i.T, loss) # 更新参数 theta = theta - alpha * gradient return theta, J_history 3、因此,在实践中,常常使用更先进的优化算法,如动量(Momentum)、总之,我们深入探讨了梯度下降法,这是一种常用的优化算法。批量梯度下降算法实现函数2、小批量梯度下降算法实现函数
def mini_batch_gradient_descent(X, y, theta, alpha, num_iters, batch_size): """ 小批量梯度下降算法实现函数 参数: X:特征矩阵,每一行代表一个训练样本的特征,每一列代表一个特征 y:目标值,向量,每个元素对应一个训练样本的目标值 theta:模型参数,向量,初始值 alpha:学习率,控制参数更新步长 num_iters:迭代次数,控制优化的迭代次数 batch_size:小批量大小,控制每次迭代使用的样本数量 返回: theta:优化后的模型参数 J_history:损失函数值的历史记录 """ m = len(y) J_history = [] # 记录损失函数值的历史记录 for iter in range(num_iters): for i in range(0, m, batch_size): # 选择一个小批量样本 X_batch = X[i:i+batch_size] y_batch = y[i:i+batch_size] # 计算损失函数值 h = np.dot(X_batch, theta) loss = h - y_batch J4、此外,学习率的选择对算法的性能至关重要,过大或过小的学习率都可能导致算法表现不佳。例如,对于非凸损失函数,梯度下降可能只能找到局部最小值而不是全局最小值。Adam、
RMSProp优化算法:
RMSProp(Root Mean Square Propagation)是一种自适应学习率的优化算法,它在Adam算法之前提出,通过计算梯度的平方的移动平均来调整学习率,从而加速收敛过程。
import numpy as npimport matplotlib.pyplot as plt# 生成示例数据np.random.seed(0)X = 2 * np.random.rand(100, 1)y = 4 + 3 * X + np.random.randn(100, 1)# 在特征矩阵 X 中添加偏置列X_b = np.c_[np.ones((100, 1)), X]# 定义激活函数(这里使用恒等函数)def identity_activation(z): return z# 定义损失函数(均方误差)def mse_loss(y_true, y_pred): return np.mean((y_true - y_pred) ** 2)# 定义批量梯度下降算法def batch_gradient_descent(X, y, theta, alpha, num_iters): m = len(y) J_history = [] # 记录损失函数值的历史记录 for iter in range(num_iters): # 计算模型预测值 y_pred = identity_activation(np.dot(X, theta)) # 计算损失函数值 J = mse_loss(y, y_pred) J_history.append(J) # 计算梯度 gradient = np.dot(X.T, (y_pred - y)) / m # 更新参数 theta = theta - alpha * gradient return theta, J_history# 初始化模型参数theta = np.random.randn(2, 1)# 设置超参数alpha = 0.01 # 学习率num_iters = 1000 # 迭代次数# 调用批量梯度下降算法训练模型theta_bgd, J_history_bgd = batch_gradient_descent(X_b, y, theta, alpha, num_iters)# 输出优化后的模型参数print("优化后的模型参数 theta:", theta_bgd)# 可视化损失函数值的变化plt.plot(range(num_iters), J_history_bgd)plt.xlabel('Iterations')plt.ylabel('Cost Function (MSE)')plt.title('Batch Gradient Descent')plt.show()执行结果:



五、损失函数是一个量化这种差距的指标,其目标是在训练过程中最小化。RMSprop等,它们是对梯度下降算法的改进和扩展。损失函数收敛等)。
具体来说,反向传播利用链式法则来计算梯度。这种方法计算量小,收敛速度快,但可能会引入噪声,导致在最小值附近震荡。在反向传播过程中,我们计算每个节点的梯度,即损失函数对该节点输入的偏导数。
计算梯度:使用当前参数计算损失函数关于这些参数的梯度。它开始于损失函数节点,并沿着计算图反向传播。通过反复进行前向传播、
一、批量梯度下降的缺点是可能陷入局部最优解,同时对内存要求较高。
更新参数:将每个参数沿着梯度的反方向移动一小步,步长由学习率控制。它的核心思想是根据目标函数的梯度方向,逐步向最陡峭的下降方向移动,以最小化目标函数。如何实现梯度下降?
二、评论啦!谢谢四连哦!好人好运连连,学习进步!工作顺利哦!
