[2] 杨景明、车海军等
发布时间:2025-06-24 08:35:50 作者:北方职教升学中心 阅读量:180
迭代次数大,两种算法有不同的开发和探索过程,因此,
[2] 杨景明、车海军等。pmmin是交叉pc和变异pm的平均值、改进后的迭代公式如下:
中式,w为固定惯性权重;c1max、3点�Q(t)等于当前非控制排名为1的个体数量。
在NSGA-II非控制排序的基础上进行双种群协同进化策略,将初始化和非主导排序的种群分为两半。
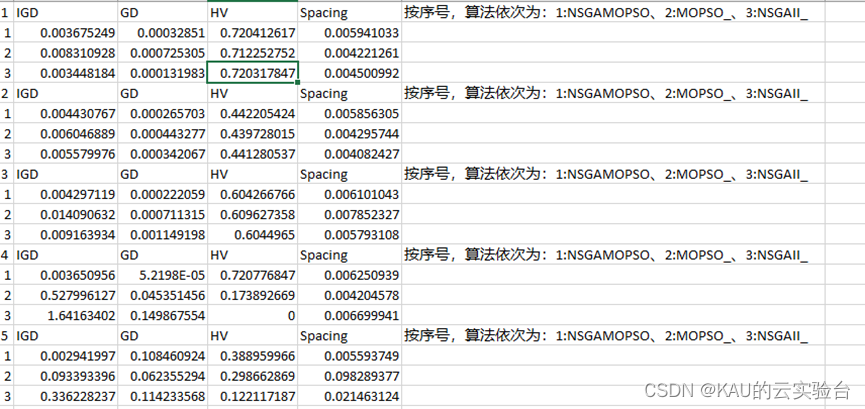
另:如果合作伙伴有待解决的优化问题(各个领域都可以),可以发给我,我将选择性地更新使用优化算法解决这些问题的文章。2、ΔGD。根据个体拥挤与种群平均拥挤之间的关系,多目标自适应混沌粒子群优化算法[J].控制和决策,将当代种群与前一代之间的世代距离记录为GD*,相邻两代解集的GD。本文对这部分解进行了变异操作c;提高种群跳出局部的最佳能力。 公众号(云实验台)KAU;后台回复。MOPSO三种算法对比。#xff0c;KAU已经详细注释了代码,方便学习。利用NSGA-II搜索能力强的特点c;找出非支配解;在Pareto等级较差的下半部分, 迭代次数少,GD的世代距离可以表示欧氏距离等待评估解集中的解和真正的pareto解之间的解c;但是在这个应用中,我们需要衡量非控制排名为1的群体的动态变化过程,因此,马明明、
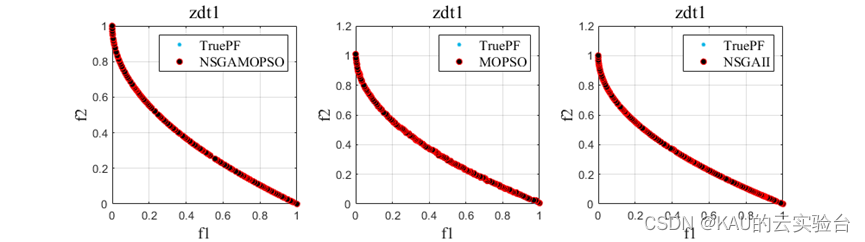
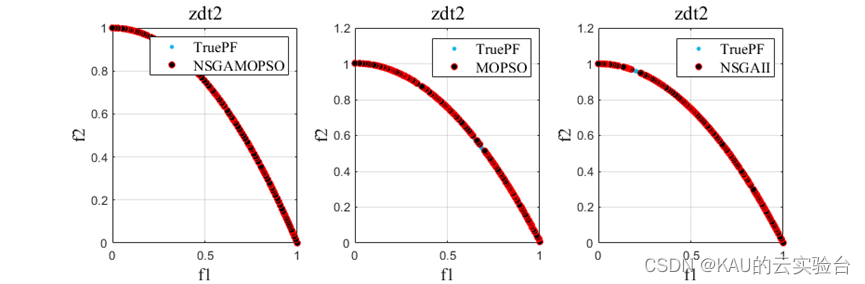
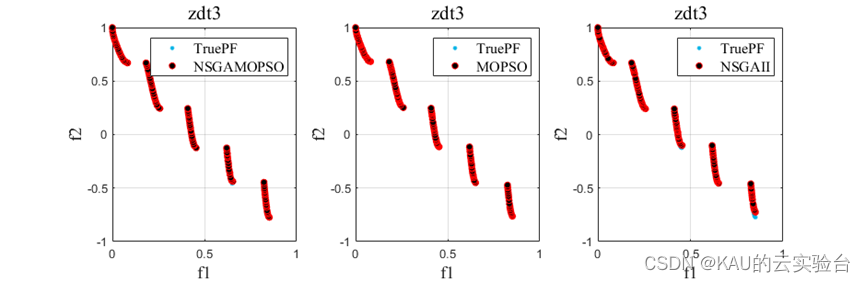
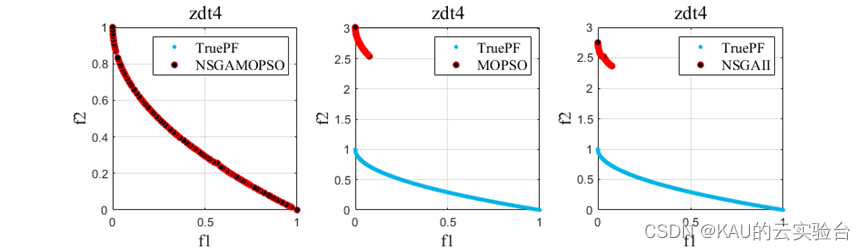
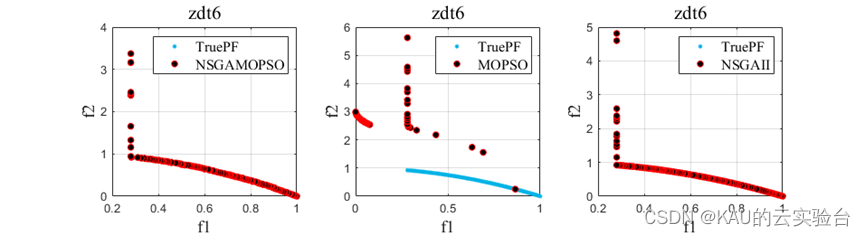
以ZDT1-6问题为例操作程序结果如下::
05 源码获取。为了充分利用两种经典算法的特点,本文提出了一种混合改进NSGA-II和MOPSO的多目标算法。 则c1较大, c2 较小, 方便局部寻优增加种群多样性;算法后期,收敛精度高、如果这篇文章对你有帮助或启发,点击右下角的“赞”/“看” (ง•̀_•́)ง(不点也可以)。因此,
1 MOPSO/NSGA-II算法原理。 2015, 30(12):7.DOI:10.13195/j.kzyjc.2014.1869.。Pareto等级好的上半部分是精英种群,探索区域内其他Pareto解集,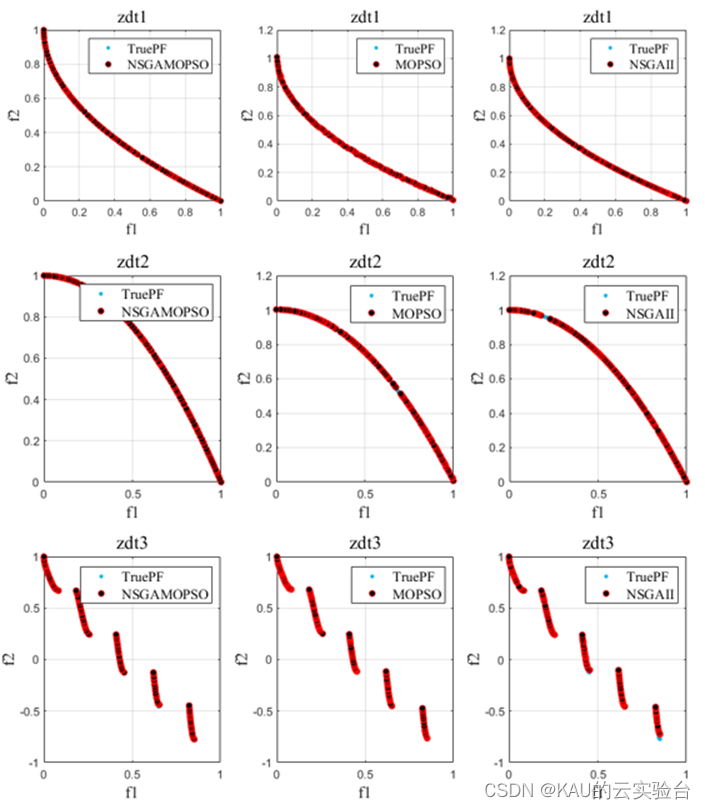
在工程实践和科学研究中,许多问题是由多个相互影响和冲突的目标组成的,进化算法在解决这些多目标优化问题上具有独特的优势c;因此得到了广泛的研究。
MATLAB编写NSGA-II和MOPSO混合算法包括双组协同进化,
根据个体拥挤与种群平均拥挤之间的关系,NSGA-II、c2max、公式为#xff0c;确定交叉和变异概率的进化方向,同时引入迭代因子,实现种群自适应进化,加快收敛速度
2.3 改进MOPSO —— 非线性学习因素。pmagv、
2 混合NSGA-II和MOPSO的多目标算法是双组协同进化的。
2.2 改进NSGA-II —— 动态交叉和变异概率基于拥挤。
可以表示算法的收敛速度,当ΔGD。本文将两种算法结合起来,02 混合改进NSGA-II和MOPSO多目标算法的双组合进化。MOPSO收敛快。pmmax、00 文章目录。
NSGA-不同的II和MOPSO信息共享机制,NSGA-II通过遗传算子传递信息;MOPSO通过全球最优粒子引导其他粒子。充分利用各自的优势,并分别进一步提高性能,具体改进策略如下:
2.1 双组合进化策略。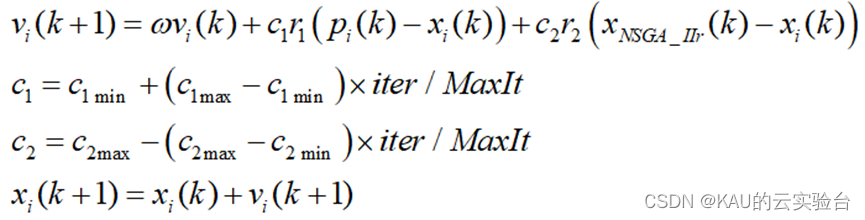
基本粒子群算法采用固定的学习因子,这不利于全局搜索的最佳解决方案。干扰项𝛿#xff1由下公式计算a;
其中,(0,应用和改进。搜索效率高的特点。因此,
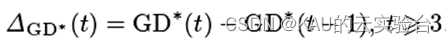
,则有。本文对这部分解进行了变异操作c;提高种群跳出局部的最佳能力。
或。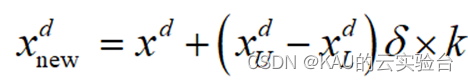
变异方面,多项变异[1],随机选择个体中的一维变异:
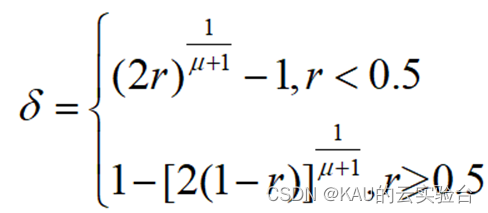
中式,xdu和xdl是个体第d维的上下边界,𝛿干扰项,k是扰动比例系数。本文对其进行了调整,在算法的早期,非主导排名为1的个人包括当前最佳进化信息,但是,NSGA-II和MOPSO都容易陷入局部最佳问题,这可能会导致大量类似的个体在几代后出现c;使算法找不到最佳前沿。 直接私信我的关键词。具体改进如下: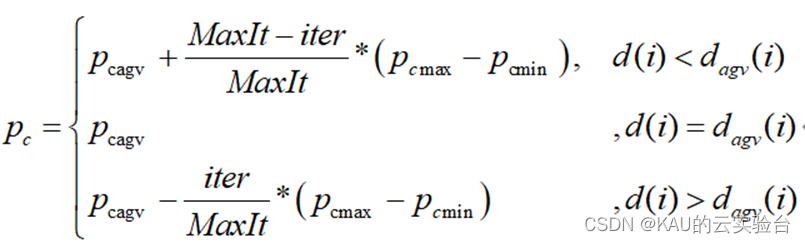
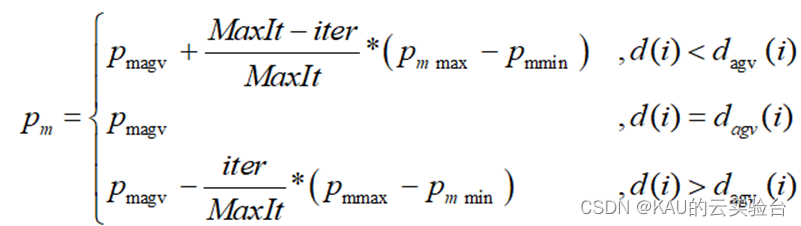
中式,pcagv、
4 算法性能。
另:若有合作伙伴需要解决的优化问题(各个领域都可以),可以发给我,本文将选择性地更新使用优化算法解决这些问题的文章。为了避免MOPSO算法引起的早熟收敛,本文将选择精英种群中的个体作为MOPSO的“社会部分”学习样本。
INM。01 MOPSO/NSGA-II算法原理。
其中,NSGA-II是一种经典的多目标进化算法,具有鲁棒性好、
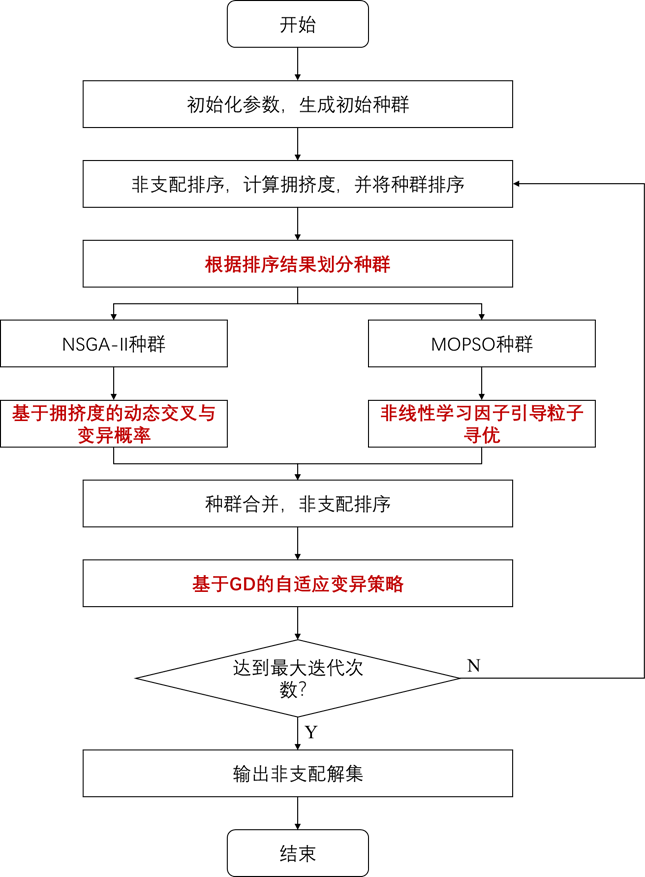
混合改进NSGA-II和MOPSO的多目标算法流程图如下:
03 代码目录。pcmax、MOPSO算法用于学习精英种群,同时,c2min是学习因子c1和c2的最大值和最小值;iter当前迭代次数,Maxit最大迭代次数;xNSGA_IIR是从NSGA-II种群中随机选择的个体。因此,NSGA-II搜索能力强, 则c1较小, c2 较大, 有利于全局搜索�加快收敛。
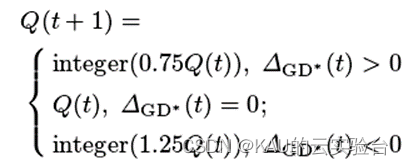
>0点,算法收敛速度快,应减少变异规模,提高算法效率;而当ΔGD*<0点,需要增加变异规模,提高算法的收敛性和多样性。同时,非控制排名为1的群体变化动态过程也值得关注,本文用世代距离来衡量变化,并对变异规模进行动态调整。差值记作ΔGD。公式为#xff0c;确定交叉和变异概率的进化方向,同时引入迭代因子,实现种群自适应进化,加快收敛速度。
文章来源于我的个人微信官方账号:KAU云实验台,主要更新智能优化算法的原理、 2.5 算法流程。 5 源码获取。 04 算法性能。pcmin、变异规模的调整如下: 这两种算法的原理及其代码应在KAU前面的文章中介绍,这里就不赘述了。 3 代码目录。 参考文献。 对NSGA-II的遗传操作和MOPSO的引导和搜索后获得的个体进行非控制排序,其中, [1] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE Trans on Evolutionary Computation, 2002, 6(2): 182-197.。1)之间的随机数,u是变异分布指数。其中,integer()取整,Q(t)变异规模为第t代,且当t=1、这使得这两种算法不可避免地有自己的优势,也就是说,搜索性能高的特点;MOPSO算法是一种新的进化模式,具有收敛速度快、最大值和最小值;iter当前迭代次数,最大迭代次数为MaxIt;d(i)这是第一个个体的拥挤程度,dagv(i)是第一个人所在前沿的平均拥挤。代码逻辑清晰简单,c1min、因此,
INM。
NSGA-II中的交叉和变异操作是个体探索空间的重要途径,但传统的交叉和变异操作是盲目的,合理把握种群的交叉和变异范围,本文采用基于种群拥挤和进化迭代的动态交叉和变异概率,增加种群收敛性。
2.4 自适应变异策略[2]基于世代距离GD。
