发布时间:2025-06-24 20:09:22 作者:北方职教升学中心 阅读量:996
查看堆顶元素
intHeapEmpty(Heap*pHeap){assert(pHeap);returnpHeap->count ==0;}HeapDataType HeapTop(Heap*pHeap){assert(!HeapEmpty(pHeap));returnpHeap->data[1];}(二)哈夫曼编码实现
#define_CRT_SECURE_NO_WARNINGS#include<stdio.h>#include<stdlib.h>#include<time.h>#include<string.h>#include<algorithm>#include<unordered_map>#include<vector>using namespace std;#defineFATHER(i)((i)/2)#defineLEFT(i)((i)*2)#defineRIGHT(i)((i)*2+1)typedefstructNode{char*c;intfreq;structNode*lchild,*rchild;}Node;template<typename T>voidSwap(T&a,T&b){T c =a;a =b;b =c;return;}//void swap(Node* a, Node* b) {// Node* c = a;// a = b;// b = c;// return;//}Node*getNewNode(intfreq,constchar*c){Node*p =(Node*)malloc(sizeof(Node));p->freq =freq;p->c =_strdup(c);p->lchild =p->rchild =NULL;returnp;}voidclear(Node*root){if(root ==NULL)return;clear(root->lchild);clear(root->rchild);free(root);return;}typedefstructheap{Node**data,**__data;intsize,count;}heap;heap*initHeap(intn){heap*p =(heap*)malloc(sizeof(heap));p->__data =(Node**)malloc(sizeof(Node*)*n);p->data =p->__data -1;p->size =n;p->count =0;returnp;}intempty(heap*h){returnh->count ==0;}intfull(heap*h){returnh->count ==h->size;}Node*top(heap*h){if(empty(h))returnNULL;returnh->data[1];}//void up_update(Node** data, int i) {// while (FATHER(i) >= 1) {// int ind = i;// if (data[i]->freq < data[FATHER(i)]->freq) {// swap(data[i], data[FATHER(i)]);//}// if (ind == i) break;// i = FATHER(i);// }// return;//}voidup_update(Node**data,inti){while(i >1&&data[i]->freq <data[FATHER(i)]->freq){Swap(data[i],data[FATHER(i)]);i =FATHER(i);}return;}voiddown_update(Node**data,inti,intn){while(LEFT(i)<=n){intind =i,l =LEFT(i),r =RIGHT(i);if(data[i]->freq >data[l]->freq)ind =l;if(RIGHT(i)<=n &&data[r]->freq <data[ind]->freq)ind =r;if(ind ==i)break;Swap(data[ind],data[i]);i =ind;}return;}voidpush(heap*h,Node*node){if(full(h))return;h->count +=1;h->data[h->count]=node;up_update(h->data,h->count);return;}voidpop(heap*h){if(empty(h))return;h->data[1]=h->data[h->count];h->count -=1;down_update(h->data,1,h->count);return;}voidclearHeap(heap*h){if(h ==NULL)return;free(h->__data);free(h);return;}Node*build_huffman_tree(Node**nodeArr,intn){heap*h =initHeap(n);for(inti =0;i <n;i++){push(h,nodeArr[i]);}Node*node1,*node2;intfreq;for(inti =1;i <n;i++){node1 =top(h);pop(h);node2 =top(h);pop(h);freq =node1->freq +node2->freq;Node*node3 =getNewNode(freq,"0");node3->lchild =node1;node3->rchild =node2;push(h,node3);}returnh->data[1];}voidoutput(Node*root){if(root ==NULL)return;output(root->lchild);//if (root->lchild == NULL && root->rchild == NULL) printf("%s : %dn",root->c,root->freq);output(root->rchild);return;}charcharArr[100];unordered_map<char*,char*>h;voidextract_huffman_code(Node*root,inti){charArr[i]=0;if(root->lchild ==NULL&&root->rchild ==NULL){h[root->c]=_strdup(charArr);return;}charArr[i -1]='0';extract_huffman_code(root->lchild,i +1);charArr[i -1]='1';extract_huffman_code(root->rchild,i +1);return;}intmain(){#defineMAX_CHAR26//1.首先用一个数组读取相关字符串及其频率Node**charArr =(Node**)malloc(sizeof(Node*)*MAX_CHAR);chararr[10];intfreq;for(inti =0;i <MAX_CHAR;i++){scanf("%s%d",arr,&freq);charArr[i]=getNewNode(freq,arr);}//2.建立哈夫曼树Node*root =build_huffman_tree(charArr,MAX_CHAR);//3.提取哈夫曼编码进入unordered_mapextract_huffman_code(root,1);//4.将unordered_map转换成vector排序,可以按照字典序输出编码vector<pair<char*,char*>>v(h.begin(),h.end());sort(v.begin(),v.end(),[&](constpair<char*,char*>&a,constpair<char*,char*>&b){returnstrcmp(a.first,b.first)<0;});for(auto&x :v){printf("%s : %sn",x.first,x.second);}return0;}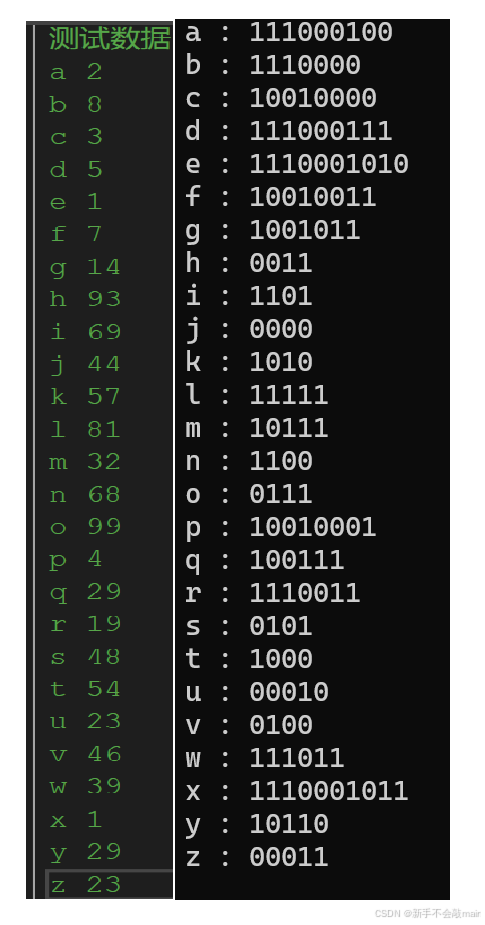
结束语
关注博主的专栏,博主会分享更多的数据结构知识!
🐾博主的数据结构专栏