返回容器可以储存的最大水量
发布时间:2025-06-24 16:57:21 作者:北方职教升学中心 阅读量:216
publicintmaxArea(int[]height){intl =0;intr =height.length-1;intarea =0;while(l<r){if(height[l]<height[r]){intcur =height[l]*(r-l);area =Math.max(area,cur);l++;}else{intcur =height[r]*(r-l);area =Math.max(area,cur);r--;}}returnarea;}funcmaxArea(height []int)int{l,r :=0,len(height)-1res :=0forl<r {ifheight[l]<height[r]{res =int(math.Max(float64(res),float64(height[l]*(r-l))))l++;}else{res =int(math.Max(float64(res),float64(height[r]*(r-l))))r--;}}returnres}三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、
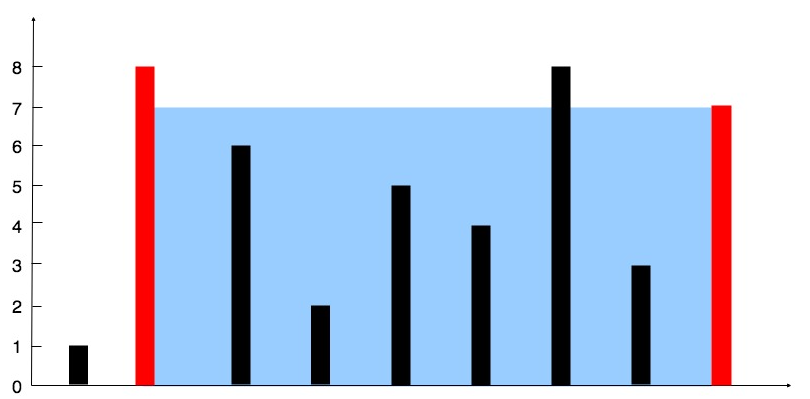
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
解放1:双指针
在每个状态下,无论长板或短板向中间收窄一格,都会导致水槽 底边宽度 −1-1−1 变短:
- 若向内 移动短板 ,水槽的短板 min(h[i],h[j])min(h[i], h[j])min(h[i],h[j]) 可能变大,因此下个水槽的面积 可能增大 。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
因此,初始化双指针分列水槽左右两端,循环每轮将短板向内移动一格,并更新面积最大值,直到两指针相遇时跳出;即可获得最大面积。
注意:答案中不可以包含重复的三元组。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
publicinttrap(int[]height){intlen =height.length;intres =0;intleft =0;intright =len-1;intleftMax =0;intrightMax =0;while(left<=right){leftMax =Math.max(leftMax,height[left]);rightMax =Math.max(rightMax,height[right]);if(leftMax<=rightMax){res+=(leftMax-height[left++]);}else{res+=(rightMax-height[right--]);}}returnres;}解法3:单调栈
栈内元素依然是单调递减。请你返回所有和为 0 且不重复的三元组。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。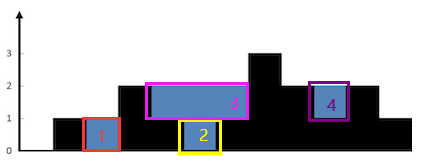
当遇到相等的时候也要出栈,但是在计算面积的时候,由于左右边界中有一条边界和当前计算的柱子高度相等,所以高度差是0,计算出来也没影响。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
解法1:双指针+交换
指针L:维护一个非零序列,L之前的元素都是非零的元素
指针R:寻找非零的元素,将其加入到L维护的序列中
publicvoidmoveZeroes(int[]nums){intl =0;intr =0;while(r<nums.length){if(nums[r]!=0)swap(nums,l++,r);r++;}}publicvoidswap(int[]nums,intl,intr){if(l ==r)return;nums[l]=nums[l]^nums[r];nums[r]=nums[l]^nums[r];nums[l]=nums[l]^nums[r];}funcmoveZeroes(nums []int){slow :=0fori,_:=rangenums{ifnums[i]!=0{tmp :=nums[slow]nums[slow]=nums[i]nums[i]=tmp slow++}}}解法2:双指针+赋值0
解法和1类似,只不过1是交换非零元素和0元素,2将非零元素全部移动到前面,后面统一赋值为0
publicvoidmoveZeroes(int[]nums){intcur =0;for(inti=0;i<nums.length;i++){if(nums[i]!=0){nums[cur++]=nums[i];}}for(;cur<nums.length;cur++){nums[cur]=0;}}盛水最多的容器
给定一个长度为 n 的整数数组 height 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
解法1:排序+双指针
先排序保证数据有序,这样就不会保存重复的数组了
接下来,外层循环确定一个 i 的值,内层循环使用左右两端向中间移动的双指针
//每个指针移动时跳过重复元素版,力扣不友好,时间还不如不跳过的快publicList<List<Integer>>threeSum(int[]nums){List<List<Integer>>res =newArrayList<>();Arrays.sort(nums);inti=0;while(i<nums.length-2){intsum =-nums[i];intj=i+1;intk=nums.length-1;while(j<k){intcur =nums[j]+nums[k];if(cur >sum){while(j<k &&nums[k]==nums[k-1])k--;k--;}elseif(cur <sum){while(j<k &&nums[j]==nums[j+1])j++;j++;}else{List<Integer>tmp =newArrayList<>();tmp.add(nums[i]);tmp.add(nums[j]);tmp.add(nums[k]);res.add(tmp);while(j<k &&nums[k]==nums[k-1])k--;k--;while(j<k &&nums[j]==nums[j+1])j++;j++;}}while(i<nums.length-2&&nums[i+1]==nums[i])i++;i++;}returnres;}//不跳过版publicList<List<Integer>>threeSum(int[]nums){List<List<Integer>>res =newArrayList<>();Arrays.sort(nums);inti=0;while(i<nums.length-2){intsum =-nums[i];intj=i+1;intk=nums.length-1;while(j<k){intcur =nums[j]+nums[k];if(cur >sum)k--;elseif(cur <sum)j++;else{List<Integer>tmp =newArrayList<>();tmp.add(nums[i]);tmp.add(nums[j]);tmp.add(nums[k]);res.add(tmp);while(j<k&&nums[k]==nums[k-1])k--;k--;}}while(i<nums.length-2&&nums[i+1]==nums[i])i++;i++;}returnres;}functhreeSum(nums []int)[][]int{res :=make([][]int,0)sort.Ints(nums)fori,v:=rangenums{ifi==len(nums)-2{break}ifi>0&&nums[i]==nums[i-1]{continue}target :=-v;l,r :=i+1,len(nums)-1forl<r {sum :=nums[l]+nums[r]ifsum>target{forl<r&&nums[r]==nums[r-1]{r--}r--;}elseifsum<target{forl<r&&nums[l]==nums[l+1]{l++}l++}else{res =append(res,[]int{v,nums[l],nums[r]})forl<r&&nums[l]==nums[l+1]{l++}l++}}}returnres}接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
注意,输出的顺序和三元组的顺序并不重要。
移动0
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。输入:[1,8,6,2,5,4,8,3,7]
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。publicinttrap(int[]height){intlen =height.length;Deque<Integer>stack =newArrayDeque<>();intres =0;for(inti=0;i<len;i++){while(!stack.isEmpty()&&height[stack.peek()]<=height[i]){intcurIndex =stack.pop();if(stack.isEmpty())break;intpreIndex =stack.peek();res+=((i-1-preIndex)*(Math.min(height[preIndex],height[i])-height[curIndex]));}stack.push(i);}returnres;}
解法1:最大前缀+最大后缀
对于每一个柱子能接的水,取决于:
- 当前柱子高度h0
- 当前柱子左侧最高的柱子h1,当前柱子右侧最高的柱子h2,取二者最小的值
- 当前柱子能接的水为:min(h1,h2)-h0
publicinttrap(int[]height){intlen =height.length;intpre[]=newint[len];intsuf[]=newint[len];pre[0]=height[0];for(inti=1;i<len;i++){pre[i]=Math.max(pre[i-1],height[i]);}suf[len-1]=height[len-1];for(inti=len-2;i>=0;i--){suf[i]=Math.max(suf[i+1],height[i]);}intsum =0;for(inti=0;i<len;i++){intlow =Math.min(pre[i],suf[i]);sum +=(low-height[i]);}returnsum;}functrap(height []int)int{iflen(height)<3{return0}leng :=len(height)leftMax :=make([]int,leng)rightMax :=make([]int,leng)leftMax[0]=height[0]fori:=1;i<len(height);i++{if(leftMax[i-1]>height[i]){leftMax[i]=leftMax[i-1]}else{leftMax[i]=height[i]}}rightMax[len(height)-1]=height[len(height)-1]fori:=len(height)-2;i>=0;i--{ifrightMax[i+1]>height[i]{rightMax[i]=rightMax[i+1]}else{rightMax[i]=height[i]}}res :=0fori:=0;i<len(height);i++{varcurHeight intif(leftMax[i]>rightMax[i]){curHeight =rightMax[i]}else{curHeight =leftMax[i]}res+=(curHeight-height[i])}returnres}解法2:双指针,解法1的节省空间的方法
解法1为了维持每个位置的左右边界最大值,使用数组来表示,可以使用双指针来代替数组。
每次双指针移动之后比较最大值,小的一方先移动。