在我们的例子中，

发布时间：2025-06-24 19:09:08  作者：北方职教升学中心  阅读量：971


就固定尺寸窗口而言，小尺寸图像上的突然移动比大尺寸图像上的更明显。OpenCV提供了一些算法实现来解决稀疏光流任务:

  • Pyramid Lucas-Kanade
  • Sparse RLOF

如果仅使用稀疏特征集意味着我们将没有关于不包含在其中的像素的运动信息。

4.4.1 理论

RLOF 算法基于 Gennert 和 Negahdaripour 在 1995 年提出的照明模型： 

        ​​​​​​​        I(x,y,t)+m\cdot I(x,y,t)+c = I(x+u,y+v,t+1)​​​​​​​

其中m,c是照明模型参数。

4.2.1 稠密金字塔 Lucas-Kanade 与 OpenCV

让我们回到 Dense Lucas-Kanade 方法。它们的理论思想以及在OpenCV 库的实际用法。稳定、实际上，光流估计并不局限于经典算法。在我们的例子中，\Delta t=1。优化过程在原始论文中进行了描述。与前面的算法一样，有一个局部运动恒定性假设，并辅以照明恒定性。现在方法已更改为：optflow.calcOpticalFlowDenseRLOF

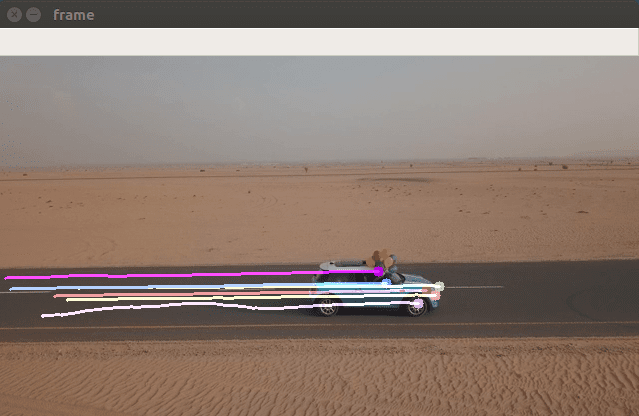
else if (method == "rlof"){    to_gray = false;    dense_optical_flow(       filename, optflow::calcOpticalFlowDenseRLOF, to_gray,        Ptr<cv::optflow::RLOFOpticalFlowParameter>(), 1.f, Size(6,6),        cv::optflow::InterpolationType::INTERP_EPIC, 128, 0.05f, 999.0f,       15, 100, true, 500.0f, 1.5f, false); // default OpenCV params}
./OpticalFlow ../videos/car.mp4 rlof

 使用上述命令运行RLOF demo 效果图如下：

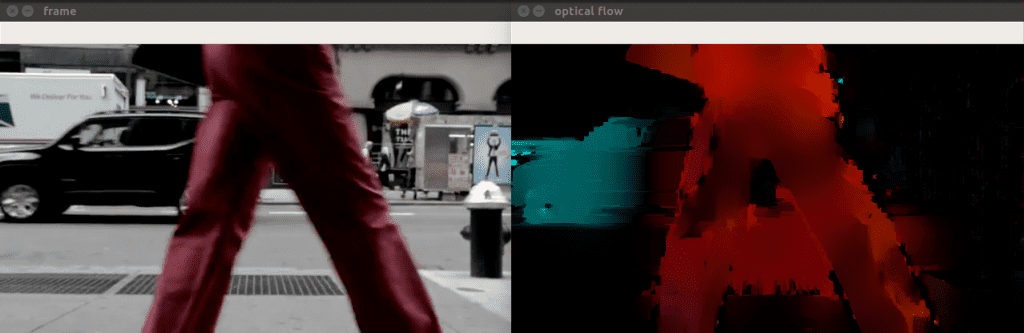
 5. 总结

本文研究了光流处理，当我们需要有关物体运动的信息时，这是必不可少的方法。它计算特定对象集的运动矢量（例如图像上检测到的角点）。这里主要关心的是找到运动矢量(\Delta x,\Delta y)，图示表示如下:

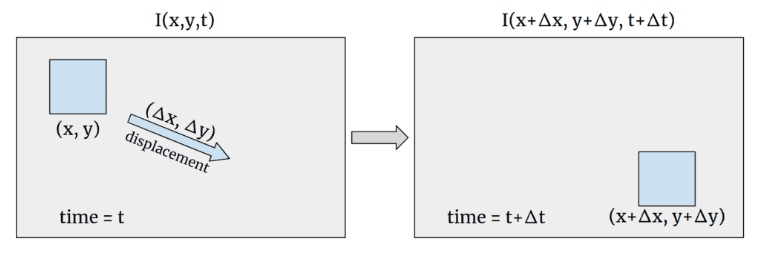
 使用泰勒级数展开我们可以得到：

                                I(x,y,t)-I _(x+\Delta x, y+ \Delta y, t+\Delta t)=0

改写为：

                                                        I_ x u+I_ y v =-I_ t

其中u = \frac{dx}{dt},v = \frac{dy}{dt}，I_ x,I_ y为图像梯度。

4.3.2 实现Farneback

OpenCV Farneback 算法需要一维输入图像，因此我们将 BRG 图像转换为灰度图。它用于查找图像中的角点，然后计算两个连续帧之间角点的运动矢量。光流的主要思想是估计由物体运动或相机移动引起的物体位移矢量。在这里，体现的是观察物体位移引起的近似多项式的差异。在main函数中调用calcOpticalFlowFarnebac包装器来实现 Farneback 的演示效果。从数学上讲，这意味着每个局部图像区域的向量[d,m,c]都是恒定的。计算出的光流显示为彩色曲线。内容涉及到讨论稀疏和稠密光流算法的相关理论和在OpenCV中的实现。

int lucas_kanade(const string& filename){    // Read the video     VideoCapture capture(filename);    if (!capture.isOpened()){        //error in opening the video input        cerr << "Unable to open file!" << endl;        return 0;    }     // Create random colors    vector<Scalar> colors;    RNG rng;    for(int i = 0; i < 100; i++)    {        int r = rng.uniform(0, 256);        int g = rng.uniform(0, 256);        int b = rng.uniform(0, 256);        colors.push_back(Scalar(r,g,b));    }     Mat old_frame, old_gray;    vector<Point2f> p0, p1;     // Read first frame and find corners in it    capture >> old_frame;    cvtColor(old_frame, old_gray, COLOR_BGR2GRAY);    goodFeaturesToTrack(old_gray, p0, 100, 0.3, 7, Mat(), 7, false, 0.04);     // Create a mask image for drawing purposes    Mat mask = Mat::zeros(old_frame.size(), old_frame.type());

在此之后就可以开始演示了。获得算法输出后，使用 HSV 颜色格式对其进行编码，得到可视化效果：

稠密光流算法输出可以编码为HSV配色方案。

首先，我们假设目标在相邻两帧之间的位移不改变属于确定目标的像素强度，这意味着I(x,y,t) = I(x+ \Delta x,y+ \Delta y,t + \Delta t)。通过这种可视化，可以清楚地了解目标和场景的动态。

0.概述

在本篇中，我们将详细了解计算视频或帧序列中光流的各种算法。通过上述分析，我们了解了一些经典算法、

代码部分用C++和Python分别展示。

4.4.2 实现 RLOF

与 Farneback 相比，RLOF 算法需要 3 通道图像，因此这里无需预处理。我们可以用一个固定大小的窗口来创建一个方程组。因此，需要一些预处理来从图像中提取特征，这将是光流计算的基础。两个帧I_1和I_2之间的像素运动差可以写为I _ 1-I _ 2\approx I_ x u+I_ y v+ I_ t. 现在，我们有两个变量u,v和一个方程，因此无法求解该方程，但可以使用一些技巧，具体技巧将在下文展开。此外，光流在动作识别任务和实时跟踪系统中也有应用。运动矢量突出显示运动的方向和大小，兴趣点（角点）用圆圈显示。 正如我们之前提到的，稠密光流算法计算稀疏特征集的运动向量，因此这里常用的方法是使用Shi-Tomasi corner detector角点检测器。

if (to_gray)    cvtColor(frame1, prvs, COLOR_BGR2GRAY);
./OpticalFlow ../videos/car.mp4 lucaskanade_dense

 得到演示效果如下，其中每个像素位移都编码为 HSV 颜色.

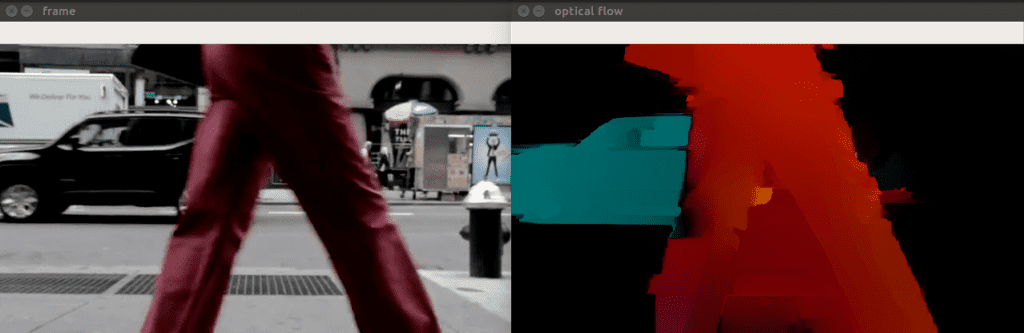
 4.3 Farneback 算法

本节将研究的是Farneback 算法，它于 2003 年被提出，用于计算图像中每个像素的光流。之后，使用有关角点位置信息基于 Lucas-Kanade 算法计算光流。

4.3.1 理论

这种方法的主要思想是用多项式近似每个像素的一些近邻：

                        ​​​​​​​        ​​​​​​​        I(x)\sim x^TAx+b^Tx+c

一般来说，在 Lucas-Canade 方法中，我们使用线性近似，

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        I(x) =b^Tx+c

之前我们只使用一阶泰勒展开。我们定义函数 I(x,y,t)，其中x,y像素坐标对应t帧时刻。

3.3 OpenCV实现

OpenCV使用改进的Shi-Tomasi算法来计算光流，实现了Lucas & Kanade 金字塔。

首先，需要读取第一个视频帧，并在必要时进行图像预处理：

template <typename Method, typename... Args>void dense_optical_flow(string filename, Method method, bool to_gray, Args&&... args){    // Read the video and first frame    VideoCapture capture(samples::findFile(filename));    if (!capture.isOpened()) {        //error in opening the video input        cerr << "Unable to open file!" << endl;    }    Mat frame1, prvs;    capture >> frame1;         # Preprocessing for exact method    if (to_gray)        cvtColor(frame1, prvs, COLOR_BGR2GRAY);    else        prvs = frame1;

演示的主要部分是一个循环，在其中计算每对新的连续图像的光流。这是一个循环过程，我们读取一个新的视频帧，并在循环中计算Shi-Tomasi特征和光流。

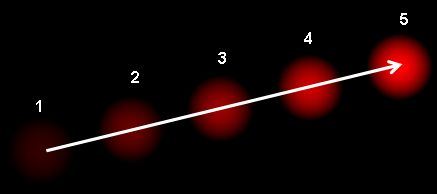
1.2 理论基础

 假设我们有一张灰度图像——像素强度矩阵。该假设有助于获得两个变量的方程的近似解。

4.1 实现与可视化

由于 OpenCV 稠密光流算法具有相同的使用模式，可以创建包装器函数以方便和避免代码重复。现在，我们正在使用二阶值提高近似的精度。

else if (method == "farneback"){    dense_optical_flow(filename, calcOpticalFlowFarneback, to_gray, 0.5,     3, 15, 3, 5, 1.2, 0); // default OpenCV params}
./OpticalFlow ../videos/car.mp4 farneback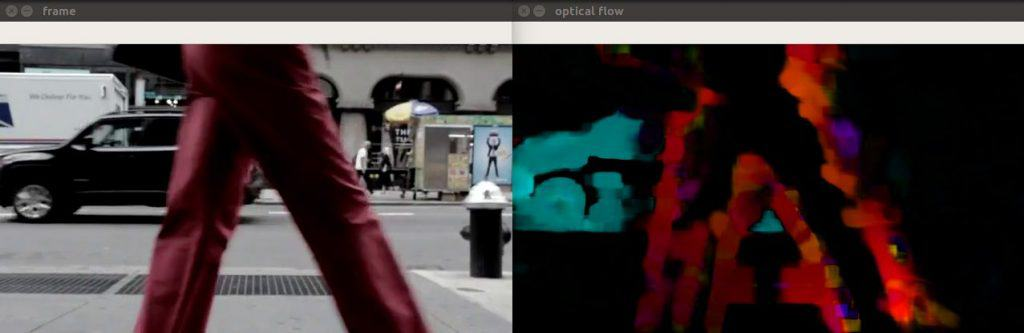

 

4.4 RLOF算法

鲁棒局部光流算法于 2016 年发布。还有阴影、使用cartToPolar 函数，可以将位移坐标(dx,dy)转换为极坐标，表示成像素位移的大小和角度。反射、这项工作的主要思想是，强度恒定性假设并不能完全反映现实世界的行为方式。我们需要创建一个所谓的图像金字塔，其中每次下一个图像都比前一个图像大一些比例因子（例如比例因子为2）。OpenCV中已经实现了一些稠密光流算法:

  • Dense Pyramid Lucas-Kanade
  • Farneback
  • PCAFlow
  • SimpleFlow
  • RLOF
  • DeepFlow
  • DualTVL1

3.稀疏光流法

3.1 Lucas-Kanade 算法

Lucas–Kanade method方法通简称为LK算法，常用于计算稀疏特征集的光流。

我们假设相邻像素具有相同的运动矢量(\Delta x, \Delta y)。

6.代码实现

#include <iostream>#include <opencv2/opencv.hpp>int main(int argc, char** argv) {    if(argc != 2) {        std::cerr << "Usage: " << argv[0] << " <video_path>" << std::endl;        return -1;    }    cv::VideoCapture cap(argv[1]);    if(!cap.isOpened()) {        std::cerr << "Error: Couldn't open the video file." << std::endl;        return -1;    }    cv::Mat oldFrame, oldGray;    std::vector<cv::Point2f> oldCorners;    // Parameters for Shi-Tomasi corner detection    int maxCorners = 100;    double qualityLevel = 0.3;    double minDistance = 7;    int blockSize = 7;    cap >> oldFrame;    cv::cvtColor(oldFrame, oldGray, cv::COLOR_BGR2GRAY);    // Detect corners in the first frame    cv::goodFeaturesToTrack(oldGray, oldCorners, maxCorners, qualityLevel, minDistance, cv::Mat(), blockSize);    // Color for optical flow    cv::Scalar color(0, 255, 0);  // Green    while(true) {        cv::Mat frame, gray;        cap >> frame;        if(frame.empty()) {            break;        }        cv::cvtColor(frame, gray, cv::COLOR_BGR2GRAY);        std::vector<cv::Point2f> newCorners;        std::vector<uchar> status;        std::vector<float> err;        // Calculate optical flow using Lucas-Kanade method        cv::calcOpticalFlowPyrLK(oldGray, gray, oldCorners, newCorners, status, err);        // Draw the motion vectors        for(size_t i = 0; i < oldCorners.size(); i++) {            if(status[i]) {                cv::line(frame, oldCorners[i], newCorners[i], color, 2);                cv::circle(frame, newCorners[i], 5, color, -1);            }        }        // Display the result        cv::imshow("Optical Flow - Lucas-Kanade", frame);        if(cv::waitKey(30) == 27) {  // Exit on pressing 'Esc' key            break;        }        // Update the previous frame and corners        oldGray = gray.clone();        oldCorners = newCorners;    }    cap.release();    cv::destroyAllWindows();    return 0;}

此代码使用 Lucas-Kanade 方法捕获视频中检测到的角点的明显运动。移动光源，简而言之，还有不同的照明。在main函数中，我们应在包装器中使用该方法：

else if (method == "lucaskanade_dense"){    dense_optical_flow(filename, optflow::calcOpticalFlowSparseToDense, to_gray, 8, 128, 0.05f, true, 500.0f, 1.5f); // default OpenCV params}

 这种方法需要一维图像作为输入，因此我们使用cvtColor将BGR图像转换为灰度图。在某些情况下，需要灰度图像，因此应将to_gray 参数设置为 True。在这里，我们可以将角度和大小分别编码为色相和值，而饱和度保持不变。基于深度学习的新方法提高了光流估计的质量，现在已经成为研究新热点。

作者基于照明模型和优化方法定义了最小化函数，该模型和优化方法迭代工作直到收敛。使用稠密光流算法可以消除这种限制，该算法应该为图像中的每个像素计算运动矢量。

执行下面的命令，可以得到效果图

./OpticalFlow ../videos/car.mp4 lucaskanade

4.稠密光流法

在本节中将介绍一些稠密光流算法，这些算法可以计算图像中每个像素的运动矢量。

while(true){    // Read new frame    Mat frame, frame_gray;    capture >> frame;    if (frame.empty())        break;    cvtColor(frame, frame_gray, COLOR_BGR2GRAY);     // Calculate optical flow    vector<uchar> status;    vector<float> err;    TermCriteria criteria = TermCriteria((TermCriteria::COUNT) + (TermCriteria::EPS), 10, 0.03);    calcOpticalFlowPyrLK(old_gray, frame_gray, p0, p1, status, err, Size(15,15), 2, criteria);    vector<Point2f> good_new;     // Visualization part    for(uint i = 0; i < p0.size(); i++)    {        // Select good points        if(status[i] == 1) {            good_new.push_back(p1[i]);            // Draw the tracks            line(mask,p1[i], p0[i], colors[i], 2);            circle(frame, p1[i], 5, colors[i], -1);        }    }     // Display the demo    Mat img;    add(frame, mask, img);    if (save) {        string save_path = "./optical_flow_frames/frame_" + to_string(counter) + ".jpg";        imwrite(save_path, img);    }    imshow("flow", img);    int keyboard = waitKey(25);    if (keyboard == 'q' || keyboard == 27)        break;     // Update the previous frame and previous points    old_gray = frame_gray.clone();    p0 = good_new;    counter++;}

简而言之，通过读取两个连续的帧，并使用goodFeaturesToTrack 函数查找第一帧上的角点。在小图像中找到的位移向量将用于下一个较大的金字塔阶段以获得更好的结果。基本上，光流任务意味着将像素的位移向量计算为两个相邻图像之间的物体位移差。因此，我们可以将方程组定义为：

                  

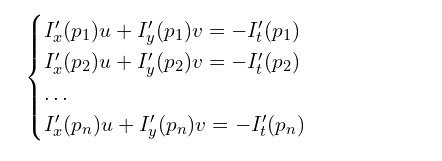
上述等式可以表示为矩阵形式：

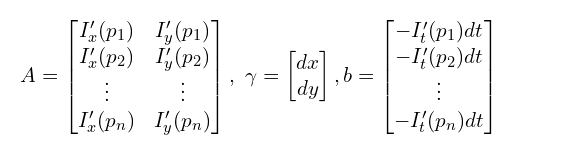
也就是矩阵表示形式为 A \gamma =b,使用最小二乘法解出\gamma

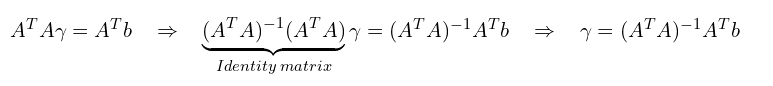
3.2 Lucas-Kanade 算法改进

由于算法的局限性，L-K光流算法确实受到突然移动的影响（相邻两帧的假设不再成立）。OpenCV中它已经作为calcOpticalFlowSparseToDense 函数实现。这是一个循环过程，对每对连续两帧图像都执行相同的操作。之后，将结果编码为 HSV 格式以进行可视化：

while (true) {    // Read the next frame    Mat frame2, next;    capture >> frame2;    if (frame2.empty())        break;     // Preprocessing for exact method    if (to_gray)        cvtColor(frame2, next, COLOR_BGR2GRAY);    else        next = frame2;     // Calculate Optical Flow    Mat flow(prvs.size(), CV_32FC2);    method(prvs, next, flow, std::forward<Args>(args)...);     // Visualization part    Mat flow_parts[2];    split(flow, flow_parts);     // Convert the algorithm's output into Polar coordinates    Mat magnitude, angle, magn_norm;    cartToPolar(flow_parts[0], flow_parts[1], magnitude, angle, true);    normalize(magnitude, magn_norm, 0.0f, 1.0f, NORM_MINMAX);    angle *= ((1.f / 360.f) * (180.f / 255.f));     // Build hsv image    Mat _hsv[3], hsv, hsv8, bgr;    _hsv[0] = angle;    _hsv[1] = Mat::ones(angle.size(), CV_32F);    _hsv[2] = magn_norm;    merge(_hsv, 3, hsv);    hsv.convertTo(hsv8, CV_8U, 255.0);         // Display the results    cvtColor(hsv8, bgr, COLOR_HSV2BGR);    if (save) {        string save_path = "./optical_flow_frames/frame_" + to_string(counter) + ".jpg";        imwrite(save_path, bgr);    }    imshow("frame", frame2);    imshow("flow", bgr);    int keyboard = waitKey(30);    if (keyboard == 'q' || keyboard == 27)        break;     // Update the previous frame    prvs = next;    counter++;}

因此，此函数读取两个连续的帧作为输入。

4.2 稠密金字塔 Lucas-Kanade算法

为了继续使用 Lucas-Kanade算法，OpenCV 不仅允许将此方法用于稀疏任务，还允许将此方法用于稠密光流计算。慢动作等。

需要指出的是，这里假设高阶泰勒级数的部分可以忽略，因此这是仅使用一阶泰勒展开式的函数近似。

首先，我们需要读取视频并从第一帧中获取 Shi-Tomasi 算法的特征。I(x,y,t)函数定义了第 t 帧时对应位置(x,y)的精确像素强度。这里的目标是是使用如下多项式近似计算位移d

                                                        I_2(x) =I_1(x-d)​​​​​​​

有关该算法及其改进的其他信息，可以在Farneback algorithm中找到。此外，这里还需要一些算法和可视化的预处理。为了恰当地显示光流，我们需要将 HSV 格式转换为 BGR 格式。

1.原理说明

1.1 什么是光流法

光流是一个视频中两个连续帧之间的逐像素运动的估计任务。这里的主要技术是使用稀疏算法输出并对整个图像进行插值，以获得每个像素的运动矢量。我们可以看看基于L-K算法官方文档的 OpenCV 算法。实践中常用的方法是使用多尺度技巧。光流常见于视频编辑器中，用于压缩、

2.光流法分类

有两种类型的光流，第一种称为稀疏光流。天气条件、该方法的主要思想基于局部运动恒定性假设，其中附近的像素具有相同的位移方向。设p_i=(x_i,y_i)为所选窗口中n个元素的像素坐标之一。

光流法可以用于物体运动信息等至关重要的许多领域。

上一篇：三亚五星级酒店夏季价格雪崩
下一篇：国家防御办公室和应急管理部门协商支持湖南省防汛抢险