(本文是增加了一个基站)

Chan算法介绍

在TDOA的解算方法上，有直接求解析解的Chan算法、
上述代码也需要注意三个地方！！！

1. 算距离差时，不加上绝对值，这样可以排除掉一半的解(两双曲线相交有2至4个交交点)
2. 计算$r_0$时可能有伪解，需要增加观测站或牺牲一定精度来排除另外一个解。

   Chan算法实现2D

   %%clc;clear;close all;format long;figure;%设置UE位置fori=1:100ue_x =randi(100);ue_y =randi(100);scatter(ue_x,ue_y,'*');hold on;%注意注意！！！基站的y不能全部相同，否则在第57行的矩阵A第二列元素全为0，Ax=C或Ax=Ds时求不出唯一解stations =[-400;200;4050;1010];%第四个基站是为了提出伪解hold on;r0_real =distance(ue_x,ue_y,stations(1,1),stations(1,2));r1_real =distance(ue_x,ue_y,stations(2,1),stations(2,2));r2_real =distance(ue_x,ue_y,stations(3,1),stations(3,2));r3_real =distance(ue_x,ue_y,stations(4,1),stations(4,2));%ri_real只是用来计算tds，实际上它会带有时钟误差，而这个误差我们不能直接得到tds =[r1_real-r0_real r2_real-r0_real,r3_real-r0_real];position =TDOA(stations,tds);scatter(position(1),position(2),'o');hold on;end%%function[position]=TDOA(stations,tds)x0 =stations(1,1);y0 =stations(1,2);x1 =stations(2,1);y1 =stations(2,2);x2 =stations(3,1);y2 =stations(3,2);x3 =stations(4,1);y3 =stations(4,2);r10 =tds(1);r20 =tds(2);r30 =tds(3);%ue对3号基站和0号基站的距离差，真实的scatter(x0,y0,120,'d','filled');text(x0,y0,'Anchor1');scatter(x1,y1,120,'d','filled');text(x1,y1,'Anchor2');scatter(x2,y2,120,'d','filled');text(x2,y2,'Anchor3');hold on;x10 =x1 -x0;x20 =x2 -x0;y10 =y1 -y0;y20 =y2 -y0;k0  =x0^2+y0^2;k1  =x1^2+y1^2;k2  =x2^2+y2^2;A =[x10 y10;x20 y20];C =-[r10;r20];D =[(k1-k0-r10^2)/2;(k2-k0-r20^2)/2];%求解Ax = r0 * C + Da =A\C;b =A\D;%求解r0A_ =a(1)^2+a(2)^2-1;B_ =a(1)*(b(1)-x0)+a(2)*(b(2)-y0);C_ =(x0 -b(1))^2+(y0 -b(2))^2;ifB_^2-A_*C_ <0position =[Nan,Nan];elser0_1 =-(B_+sqrt(B_^2-A_*C_))/A_;r0_2 =-(B_-sqrt(B_^2-A_*C_))/A_;X1 =a *r0_1 +b;X2 =a *r0_2 +b;%剔除错误解：方法一：UE和基站时钟尽量同步。
   TDOA算法原理
   TDOA(Time Difference of Arrival)——时间差到达算法，利用了几何数学中双曲线的特点—— 双曲线上的任意点到达两焦点的距离差是固定值。
   
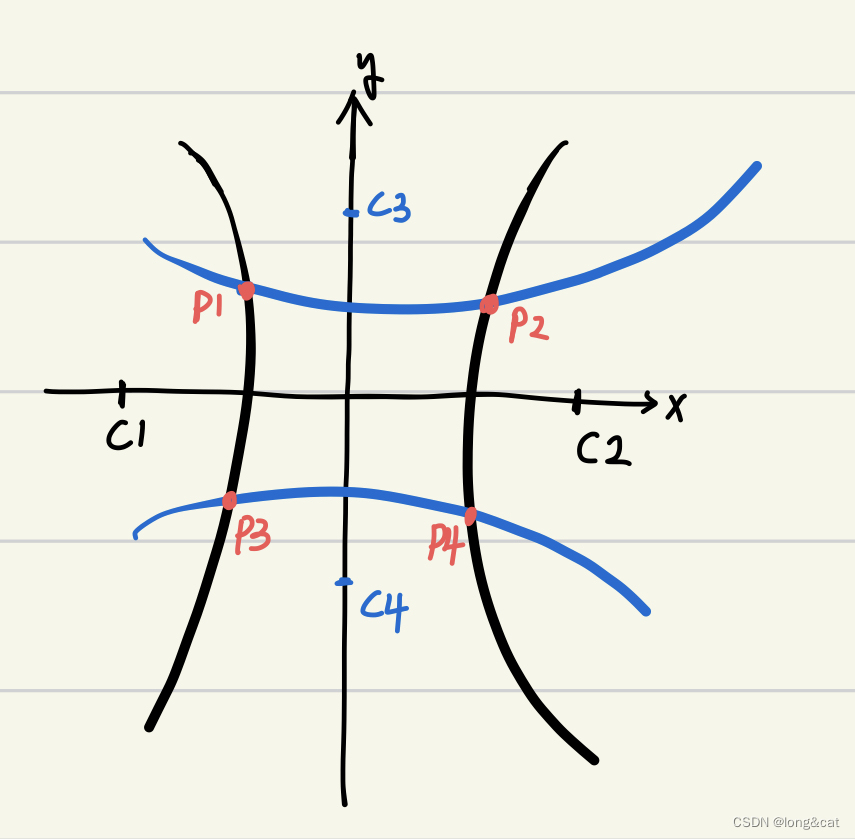
   $$P_1{C}_1=c\cdot (t_{11}+\Delta t)$$其中$\Delta t$是UE和基站之间的钟差(在UE与基站不完全同步的情况下)，这个钟差我们没法直接获得。(本文是增加了一个基站)。方法二：增加观测站(本例使用)ifabs(r40-(distance(X1(1),X1(2),X1(3),x4,y4,z4)-distance(X1(1),X1(2),X1(3),x0,y0,z0)))<1e-8position =X1;elseposition =X2;endend%%functiondist =distance(x1,y1,z1,x2,y2,z2)dist =sqrt((x1-x2)^2+(y1-y2)^2+(z1-z2)^2);end

   这份代码是随机生成了100个三维点，然后使用Chan算法解算位置。

   Chan算法实现3D

   %%clc;clear;close all;format long;% tmp = unifrnd(0,255,4,2);% x1 = tmp(1,1); y1 = tmp(1,2);  % Anchor1% x2 = tmp(2,1); y2 = tmp(2,2);  % Anchor2% x3 = tmp(3,1); y3 = tmp(3,2);  % Anchor3figure;%随机生成100个UE位置，并对其进行TDOA计算correct_sum =0;uncorrect_sum =0;fori=1:100ue_x =randi(60)+randn();ue_y =randi(60)+randn();ue_z =randi(60)+randn();scatter3(ue_x,ue_y,ue_z,120,'*');hold on;%注意注意！！！基站的z不能全部相同，否则在第67行的矩阵A第三列元素全为0，Ax=C或Ax=Ds时求不出唯一解stations =[-4005;20015;40505;005;101010];r0_real =distance(ue_x,ue_y,ue_z,stations(1,1),stations(1,2),stations(1,3));r1_real =distance(ue_x,ue_y,ue_z,stations(2,1),stations(2,2),stations(2,3));r2_real =distance(ue_x,ue_y,ue_z,stations(3,1),stations(3,2),stations(3,3));r3_real =distance(ue_x,ue_y,ue_z,stations(4,1),stations(4,2),stations(4,3));r4_real =distance(ue_x,ue_y,ue_z,stations(5,1),stations(5,2),stations(5,3));tds =[r1_real-r0_real r2_real-r0_real r3_real-r0_real r4_real-r0_real];position =TDOA(stations,tds);ifdistance(position(1),position(2),position(3),ue_x,ue_y,ue_z)<1e-8correct_sum =correct_sum +1;elseuncorrect_sum =uncorrect_sum +1;endscatter3(position(1),position(2),position(3),'o','r');hold on;end%%function[position]=TDOA(stations,tds)x0 =stations(1,1);y0 =stations(1,2);z0 =stations(1,3);x1 =stations(2,1);y1 =stations(2,2);z1 =stations(2,3);x2 =stations(3,1);y2 =stations(3,2);z2 =stations(3,3);x3 =stations(4,1);y3 =stations(4,2);z3 =stations(4,3);x4 =stations(5,1);y4 =stations(5,2);z4 =stations(5,3);r10 =tds(1);r20 =tds(2);r30 =tds(3);r40 =tds(4);scatter3(x0,y0,z0,120,'d','filled');text(x0,y0,z0,'Station1');hold on;scatter3(x1,y1,z1,120,'d','filled');text(x1,y1,z1,'Station2');hold on;scatter3(x2,y2,z2,120,'d','filled');text(x2,y2,z2,'Station3');hold on;scatter3(x3,y3,z3,120,'d','filled');text(x3,y3,z3,'Station4');hold on;hold on;% r21 represents the TDOA between anchor1 and anchor2% r31 represents the TDOA between anchor1 and anchor3x10 =x1 -x0;x20 =x2 -x0;x30 =x3 -x0;y10 =y1 -y0;y20 =y2 -y0;y30 =y3 -y0;z10 =z1 -z0;z20 =z2 -z0;z30 =z3 -z0;k0  =x0^2+y0^2+z0^2;k1  =x1^2+y1^2+z1^2;k2  =x2^2+y2^2+z2^2;k3  =x3^2+y3^2+z3^2;A =[x10 y10 z10;x20 y20 z20;x30 y30 z30];C =-[r10;r20;r30];D =[(k1-k0-r10^2)/2;(k2-k0-r20^2)/2;(k3-k0-r30^2)/2];%求解Ax = r0 * C + Da =A\C;b =A\D;%求解r0A_ =a(1)^2+a(2)^2+a(3)^2-1;B_ =a(1)*(b(1)-x0)+a(2)*(b(2)-y0)+a(3)*(b(3)-z0);C_ =(x0 -b(1))^2+(y0 -b(2))^2+(z0 -b(3))^2;r0_1 =-(B_+sqrt(B_^2-A_*C_))/A_;r0_2 =-(B_-sqrt(B_^2-A_*C_))/A_;X1 =a *r0_1 +b;X2 =a *r0_2 +b;%剔除错误解：方法一：UE和基站时钟尽量同步。

上述代码的运行结果

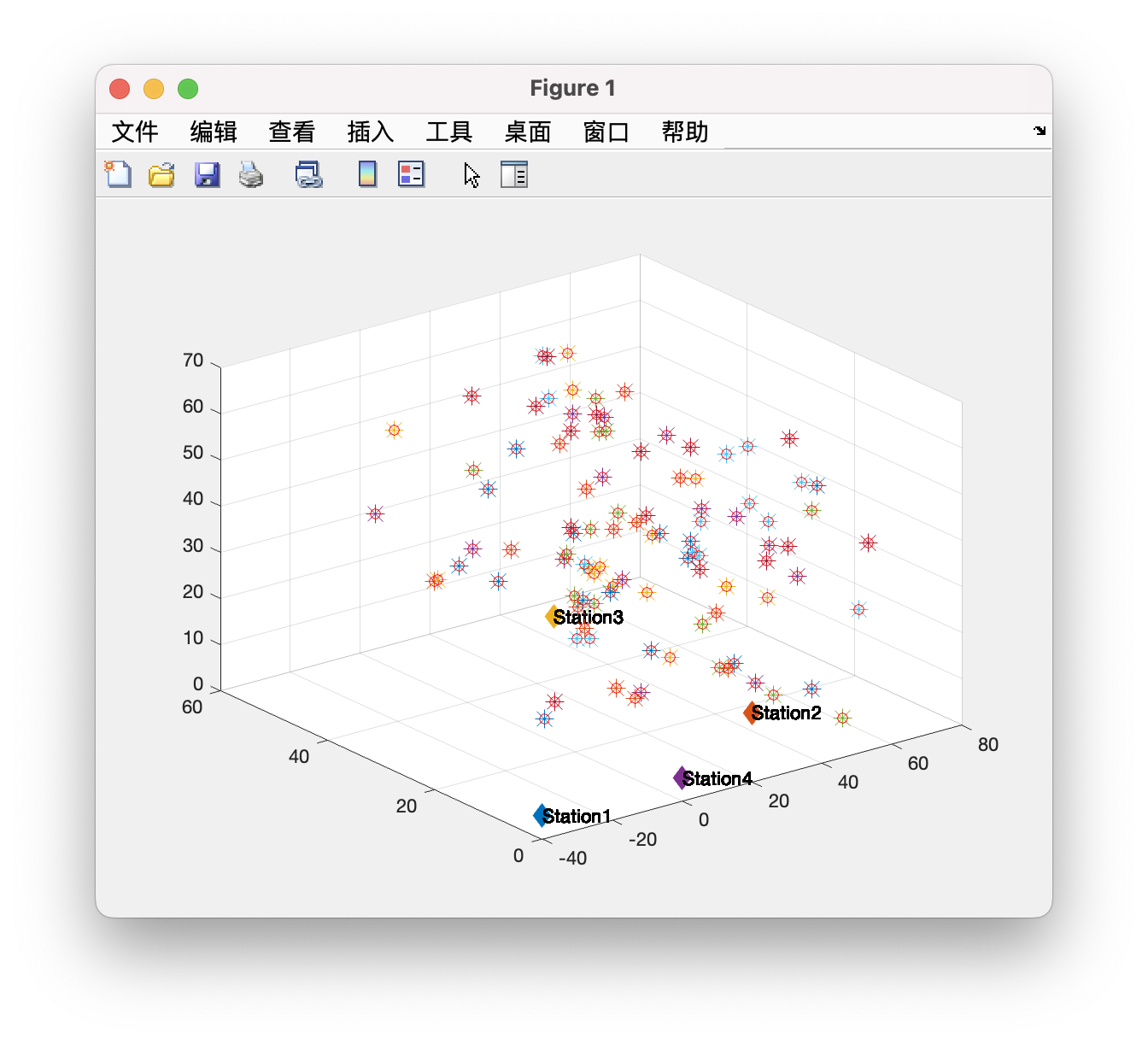
经过测试，所有的解算误差都小于 $10^{-8}$